如图所示,正方形 与矩形
与矩形 所在平面互相垂直,
所在平面互相垂直, ,点
,点 为
为 的中点.
的中点.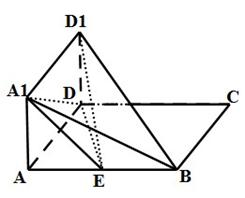
(1)求证: ∥平面
∥平面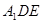 ;
;
(2)求证: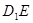
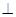
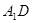 ;
;
(3)在线段 上是否存在点
上是否存在点 ,使二面角
,使二面角 的大小为
的大小为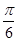 ?若存在,求出
?若存在,求出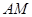 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
在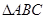 中,已知
中,已知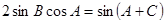
(1)求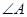 ;
;
(2)若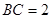 ,
,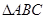 的面积是
的面积是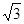 ,求
,求 .
.
在平面直角坐标系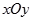 中,已知圆
中,已知圆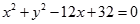 的圆心为
的圆心为 ,过点
,过点 且斜率为
且斜率为 的直线与圆
的直线与圆 相交于不同的两点
相交于不同的两点 .
.
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)以OA,OB为邻边作平行四边形OADB,是否存在常数 ,使得直线OD与PQ平行?如果存在,求
,使得直线OD与PQ平行?如果存在,求 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
已知以点C (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M、N,若OM=ON,求圆C的方程.
已知圆C: 直线
直线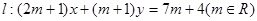
(1)证明:不论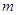 取何实数,直线
取何实数,直线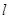 与圆C恒相交;
与圆C恒相交;
(2)求直线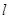 被圆C所截得的弦长的最小值及此时直线
被圆C所截得的弦长的最小值及此时直线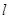 的方程.
的方程.