2014年“双节”期间，高速公路车辆较多．某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/t）分成六段：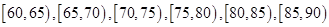
后得到如图的频率分布直方图．
（1）求这40辆小型车辆车速的众数和中位数的估计值．
（2）若从车速在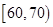
的车辆中任抽取2辆，求车速在
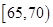的车辆恰有一辆的概率．
（本小题满分12分）已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如下表：
若抽取学生n人，成绩分为A（优秀）、B（良好）、C（及格）三个等级，设x，y分别表示数学成绩与地理成绩，例如：表中数学成绩为B等级的共有20+18+4=42人，已知x与y均为B等级的概率是0．18．
（1）若在该样本中，数学成绩优秀率是30%，求a，b的值；
（2）在地理成绩为C等级的学生中，已知a≥10，b≥8，求数学成绩为A等级的人数比C等级的人数少的概率．
如图所示，在正方体
中，
分别是棱
的中点．
（Ⅰ）证明：平面
平面
；
（Ⅱ）证明：
//平面；
（Ⅲ）若正方体棱长为1，求四面体
的体积．
已知函数
的最大值为了3，函数
的图象的相邻两对称轴间的距离为2，在
轴上的截距为2。
（1）求函数的解析式；
（2）求函数的单调递增区间。
已知数列
的前n项和
（其中c，k为常数），且
2=4，6=83
（Ⅰ）求
；
（Ⅱ）求数列
的前n项和Tn．
（本小题满分14分）已知焦点在
轴，顶点在原点的抛物线
经过点
，以抛物线上一点
为圆心的圆过定点
（0，1），记
为圆与
轴的两个交点．
（1）求抛物线的方程；
（2）当圆心在抛物线上运动时，试判断
是否为一定值？请证明你的结论；
（3）当圆心在抛物线上运动时，记
，
，求
的最大值．