小明有5张写着不同数字的卡片，请你按要求抽出卡片，完成下列各问题：
（1）从中取出2张卡片，使这2张卡片上数字的乘积最大，如何抽取？最大值是多少?
答：我抽取的2张卡片是 、 ，乘积的最大值为 ．
（2）从中取出2张卡片，使这2张卡片上数字相除的商最小，如何抽取？最小值是多少?
答：我抽取的2张卡片是 、 ，商的最小值为 ．
（3）从中取出2张卡片，使这2张卡片上数字组成一个最大的数，如何抽取？最大的数是多少?
答：我抽取的2张卡片是 、 ，组成的最大数为 ．
（4）从中取出4张卡片，用学过的运算方法，使结果为24．如何抽取？写出运算式子．
（写出一种即可）．
答：我抽取的4张卡片是 、 、 、 ，
算24的式子为 ．
如图，B、C、E三点在一条直线上，⊿ABC和⊿DCE都为等边三角形，连接AE、DB、
（1）试说出 AE=BD的理由、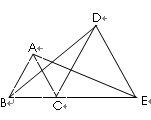
（2）如果把⊿DCE绕C点顺时针旋转一个角度，使B、C、E不在一条直线上,（1)中的结论还成立吗？（只回答，不说理由）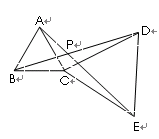
（3）在（2）中若AE、BD相交于P, 求∠APB的度数、
如图1，已知l1∥l2，MN分别和直线l1、l2交于点A、B，ME分别和直线l1、l2交于点C、D．点P在MN上（P点与A、B、M三点不重合）．∠PDB=α，∠PCA=β，∠CPD=γ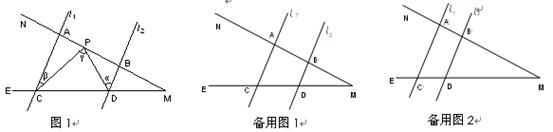
（1）如果点P在A、B两点之间运动时α、β、γ之间有何数量关系？请说明理由．
（2）如果点P在A、B两点外侧运动时α、β、γ之间有何数量关系？请说明理由．
已知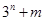
能被13整除,求证
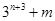也能被13整除、
①已知
求
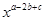的值。
②若n满足(n-2010)2+(2011-n)2=3，求(n-2010)(2011-n)的值。
③已知：多项式
中不含xy项．
求: 
的值、
观察下列各式：（x-1）(x+1)=x
–1
(x-1)(x+x+1)=x
-1
(x-1)(x+x+x+1)=x
-1
(x-1)(x+x+x+x+1)=x
-1
(1) 根据前面各式的规律可得：（x-1）(x
+x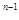
+…+x+1)= 、(其中n为正整数)
（2）根据（1）求：1+2+2+2+…+2
+2
的值，并求出它的个位数字。