(本小题满分12分)设函数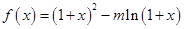 ,
, .
.
(1)当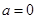 时,
时,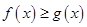 在
在 上恒成立,求实数
上恒成立,求实数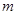 的取值范围;
的取值范围;
(2)当 时,若函数
时,若函数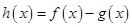 在
在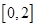 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数 的取值范围;
的取值范围;
(3)是否存在常数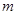 ,使函数
,使函数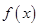 和函数
和函数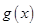 在公共定义域上具有相同的单调性?若存在,求出
在公共定义域上具有相同的单调性?若存在,求出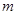 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
如图,在四棱锥P—ABCD中,底面ABCD是边长为4的菱形,且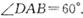 菱形ABCD的两条对角线的交点为O,PA=PC,PB=PD且PO= 3.点E是线段PA的中点,连接EO,EB,EC
菱形ABCD的两条对角线的交点为O,PA=PC,PB=PD且PO= 3.点E是线段PA的中点,连接EO,EB,EC
(I)证明:直线0E//平面PBC;
(II)求二面角E-BC-D的大小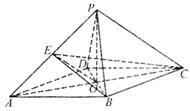
已知 中,内角A、B、C所对边的长分别是a、b、c,且点
中,内角A、B、C所对边的长分别是a、b、c,且点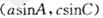 在直线
在直线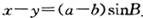 上.
上.
(I)求角C的大小;
(II)若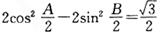 ,且A<B,求.
,且A<B,求.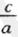 的值.
的值.
甲乙两物体分别从相距70米的两处同时运动,甲第一分钟走2米,以后每分钟比前一分钟多走1米,乙每分钟走5米。
(1).甲乙开始运动后几分钟相遇?
(2)如果.甲乙到达对方起点后立即折返,甲继续每分钟比前一分钟多走1米,乙继续每分钟走5米,那么开始运动几分钟后第二次相遇。
已知函数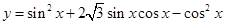 ,
,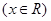
(1)求最小正周期(2)单调增区间
(3)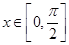 时,求函数的值域。
时,求函数的值域。
设数列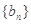 满足:
满足: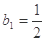 ,
,
(Ⅰ)求证: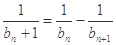 ;
;
(Ⅱ)若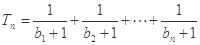 ,对任意的正整数
,对任意的正整数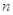 ,
,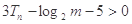 恒成立,
恒成立,
求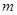 的取值范围.
的取值范围.