(本小题满分10分)如图,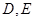 分别为
分别为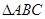 的边
的边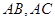 上的点,且不于
上的点,且不于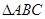 的顶点重合.已知
的顶点重合.已知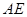 的长为
的长为 的长为
的长为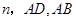 的长是关于
的长是关于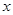 的方程
的方程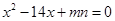 的两个根.
的两个根.
(Ⅰ)证明: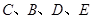 四点共圆;
四点共圆;
(Ⅱ)若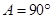 ,且
,且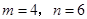 ,求
,求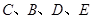 所在圆的半径.
所在圆的半径.
(本小题为必做题,满分10分)如图,在四棱锥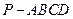 中,底面
中,底面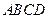 为矩形,侧棱
为矩形,侧棱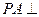 底面
底面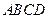 ,
,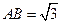 ,
,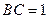 ,
,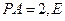 为
为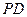 的中点.
的中点.
(1) 求直线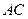 与
与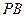 所成角的余弦值;
所成角的余弦值;
(2) 在侧面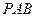 内找一点
内找一点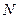 ,使
,使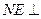 面
面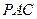 ,并求出点
,并求出点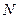 到
到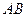 和
和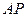 的距离.
的距离.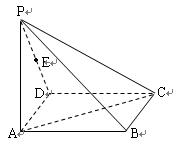
(本小题为选做题,满分10分)
设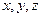 为正数,证明:
为正数,证明: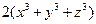 ≥
≥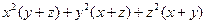 .
.
(本小题为选做题,满分10分)
设点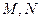 分别是曲线
分别是曲线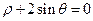 和
和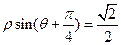 上的动点,求动点
上的动点,求动点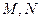 间的最小距离.
间的最小距离.
(本小题为选做题,满分10分)
已知矩阵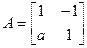 ,其中
,其中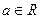 ,若点P(1,1)在矩阵A的变换下得到点
,若点P(1,1)在矩阵A的变换下得到点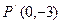 ,
,
(1)求实数a的值;(2)求矩阵A的特征值及特征向量.
(本小题为选做题,满分10分)
如图,AB是半圆的直径,C是AB延长线上一点,CD
切半圆于点D,CD=2,DE⊥AB,垂足为E,且E是
OB的中点,求BC的长.