如图,Rt△ABC中,AC=BC= ,CD⊥AB,沿CD将△ABC折成600的二面角A―CD―B ,求折叠后点A到平面BCD的距离。
,CD⊥AB,沿CD将△ABC折成600的二面角A―CD―B ,求折叠后点A到平面BCD的距离。
 C. C
C. C D
D
A. D. B. A. B
计算( 每题 6分,共18分)
(1)2log525 + 3log264(2)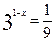 (3)
(3) 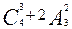 =
=
(本题满分14分)数列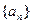 的前
的前 项和为
项和为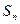 ,且
,且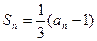
(1)求  ,
, 及
及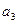 ;
;
(2)证明:数列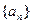 是等比数列,并求
是等比数列,并求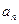 .
.
(本题满分12分)△ABC中,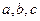 是A,B,C所
是A,B,C所 对的边,S是
对的边,S是 该三角形的面积,且
该三角形的面积,且

( 1)求∠B的大小;
1)求∠B的大小;
(2)若 =4,
=4, ,求
,求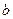
 的值。
的值。
(本题满分12分)已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4, 3),M是BC边上的中点。
3),M是BC边上的中点。
(1)求AB边所在的直线方程;
(2)求中线AM的长。