我们引入定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图1,若PA=PB,则点P为△ABC的准外心.
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD=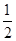 AB,求∠APB的度数.
AB,求∠APB的度数.
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.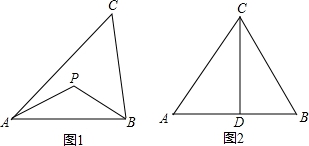
某班到毕业时共结余经费1800元,班委会决定拿出不少于1500元但不超过1530元的资金为老师购买纪念品,其余资金用于在毕业晚会上给50位同学每人购买一件文化衫或一本相册作为纪念品.已知每件文化衫比每本相册贵9元,用200元恰好可以买到2件文化衫和5本相册求每件文化衫和每本相册的价格分别为多少元?
有几种购买文化衫和相册的方案?哪种方案用于购买老师纪念品的资金更充足?
如图,在平面直角坐标系中,△ABC和△A1B1C1关于点E成中心对称.画出对称中心E,并写出点E、A、C的坐标
P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P2(a+6,b+2),请画出上述平移后的△A2B2C2,并写出点A2、C2的坐标;
判断△A2B2C2和△A1B1C1的位置关系(直接写出结果).

如图,把一个转盘分成四等份,依次标上数字1、2、3、4,若连续自由转动转盘二次,指针指向的数字分别记作 把
把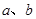 作为点
作为点 的横、纵坐标.
的横、纵坐标.
求点A(a,b)的个数;
求点A(a,b)在函数
 的图象上的概率.
的图象上的概率.
为了改进银行的服务质量,随机抽查了30名顾客在窗口办理业务所用的时间(单位:分钟).下图是这次调查得到的统计图.请你根据图中的信息回答下列问题: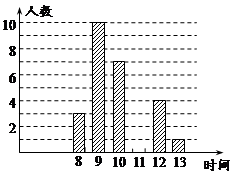
办理业务所用的时间为11分钟的人数是;
补全条形统计图;
这30名顾客办理业务所用时间的平均数是分钟.
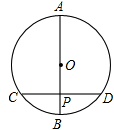
如图,⊙O的直径AB垂直于弦CD,垂足P是OB的中点,CD=6 ,求直径AB的长.