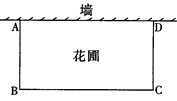
我国为了维护队钓鱼岛P的主权,决定对钓鱼岛进行常态化的立体巡航.在一次巡航中,轮船和飞机的航向相同(AP∥BD),当轮船航行到距钓鱼岛20km的A处时,飞机在B处测得轮船的俯角是45°;当轮船航行到C处时,飞机在轮船正上方的E处,此时EC=5km.轮船到达钓鱼岛P时,测得D处的飞机的仰角为30°.试求飞机的飞行距离BD(结果保留根号).
某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量 (件)与销售单价
(件)与销售单价 (元)符合一次函数
(元)符合一次函数 ,且
,且 时,
时, ;
; 时,
时, .(1)求一次函数
.(1)求一次函数 的表达式;
的表达式;
(2)若该商场获得利润为 元,试写出利润
元,试写出利润 与销售单价
与销售单价 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价 的范围.
的范围.
如图有一座抛物线形拱桥,桥下面在正常水位是AB宽20m,水位上升3m就达到警戒线CD,这是水面宽度为10m。(1)在如图的坐标系中求抛物线的解析式。(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?
|
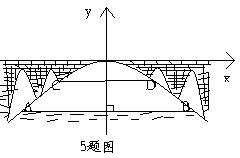
如图,在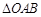 中,
中,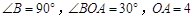 ,将
,将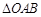 绕点
绕点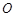 按逆时针方向旋转至
按逆时针方向旋转至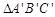 ,
,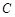 点的坐标为
点的坐标为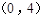 .(1)求
.(1)求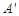 点的坐标;
点的坐标;
(2)求过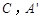 ,
,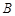 三点的抛物线
三点的抛物线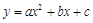 的解析式;
的解析式;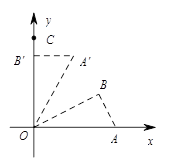
改革开放以来,某镇通过多种途径发展地方经济,1995年该镇年国民生产总值为2亿元,根据测算,该镇国民生产总产值为5亿元时,可达到小康水平。(1)若从1996年开始,该镇国民生产总值每年比上一年增加0.6亿元,该镇通过几年可达到小康水平?(2)设以2001年为第一年,该镇第x年的国民生产总值为y亿元,y与x之间的关系是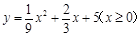 该镇那一年的国民生产总值可在1995年的基础上翻两番(即达到1995年的年国民生产总值的4倍)?
该镇那一年的国民生产总值可在1995年的基础上翻两番(即达到1995年的年国民生产总值的4倍)?
张大爷要围成一个矩形花圃.花圃的一边利用足够长的墙另三边用总长为32米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD.设AB边的长为x米.矩形ABCD的面积为S平方米.
(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围)
(2)当x为何值时,S有最大值?并求出最大值.