景山中学开展演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.

(1)根据图填写下表;
| |
平均分 |
中位数 |
众数 |
极 差 |
方 差 |
| 九(1)班 |
85 |
|
85 |
|
|
| 九(2)班 |
80 |
|
|
|
(2)结合两班复赛成绩的平均数和中位数、极差、方差,分析哪个班级的复赛成绩较好?
(3)如果在每班参加复赛的选手中分别选出2人参加决赛,你认为哪个班的实力更强一些,说明理由.
施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系(如图所示).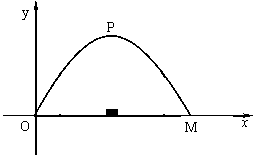
(1)求出这条抛物线的函数解析式,并写出自变量x的取值范围;
(2)隧道下的公路是双向等宽行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽2.5米、高5米的特种车辆?请通过计算说明;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”CDAB,使A、D点在抛物线上.B、C点在地面OM线上(如图所示).为了筹备材料,需求出“脚手架”三根钢管AB、AD、DC的长度之和的最大值是多少,请你帮施工队计算一下.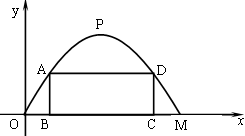
西瓜经营户以2元/kg的价格购进一批小型西瓜,以3元/kg的价格出售,每天可售出200kg.为了尽快售罄,该经营户决定降价促销,经调查发现,这种小型西瓜每降价0.1元/kg,每天可多售出40kg.另外,经营期间每天还需支出固定成本24元.该经营户要想每天至少盈利200元,应将每千克小型西瓜的售价降低多少元?
如图,△ABC内接于⊙O,且AB=AC,BD是⊙O的直径, AD与BC交于点E,F在DA的延长线上,且BF=BE.
|

 ,求⊙O的直径.
,求⊙O的直径.
台风是夏季影响城市安全的重要因素之一.如图,坡上有一棵与水平面EF垂直的大树AB,被台风吹过后,大树倾斜并折断倒在山坡上,大树顶部B接触到坡面上的D点.已知山坡的坡角∠AEF=30°,量得∠BAC=45°,∠ADC=60°,AD=4米.
(1)求∠CAE的度数;(2)求这棵大树折断前的高度AB(结果精确到0.1米).
一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:(单位:分)
(1)填写表格中的空档;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.从标准分看,标准分大的考试成绩更好.请问A同学在本次考试中,数学与英语哪个学科考得更好?