已知：
ABCD的两边AB，AD的长是关于x的方程
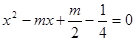的两个实数根．
（1）当m为何值时，四边形ABCD是菱形？求出这时菱形的边长；
（2）若AB的长为2，那么
ABCD的周长是多少？
如图是规格为8×8的正方形网格，请在所给网格中按下列要求操作：
（1）在网格中建立平面直角坐标系，使A点坐标为（﹣2，4），B点坐标为（﹣4，2）；
（2）在第二象限内的格点上画一点C，使点C与线段AB组成一个以AB为底的等腰三角形，且腰长是无理数，则C点坐标是________；
（3）△ABC的周长=_________（结果保留根号）；
（4）画出△ABC关于关于y轴对称的△A′B′C′．
为加强与家长的沟通，某校在家长会到来之前需印刷《致家长的一封信》等材料以作宣传，该校的印刷任务原来由甲复印店承接，其收费y（元）与印刷页数x（页）的函数关系如图所示．
（1）从图象中可看出：印刷超过500页部分每页收费 元；
（2）现在乙印刷厂表示：每页0.15元收费．另收200元的制版费，乙印刷厂收费y（元）与印刷页数x（页）的函数关系为 ；
（3）在给出的坐标系内画出（2）中的函数图象，并结合函数图象回答印刷页数在3000页左右应选择哪个印刷店？
某中学为了了解全校的耗电情况抽查了10天中全校每天的耗电量，数据如下表：
度数 90 93 102 113 114 120
天数 11 2 31 2
（1）写出上表中数据的众数和平均数．
（2）根据上题获得的数据，估计该校一个月的耗电量（按30天计算）．
（3）若当地每度电的价格是0.5元，写出该校应付电费y（元）与天数x（x取正整数，单位：天）的函数关系式．
我市为加快美丽乡村建设，建设秀美幸福抚州，对A、B两类村庄进行了全面改建．根据预算，建设一个A类美丽村庄和一个B类美丽村庄共需资金300万元；甲镇建设了2个A类村庄和5个B类村庄共投入资金1140万元．
（1）建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元？
（2）乙镇3个A类美丽村庄和4个B类村庄改建共需资金多少万元？
如图，一段街道的两边缘所在直线分别为AB，PQ，并且AB∥PQ．建筑物的一端DE所在的直线MN⊥AB于点M，交PQ于点N，步行街宽MN为13.4米，建筑物宽DE为6米，光明巷宽EN为2.4米．小亮在胜利街的A处，测得此时AM为12米，求此时小亮距建筑物拐角D处有多远？