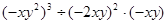如图，□ABCD中，E是CD的延长线上一点，BE与AD交于点F，
。
（1）求证：△ABF∽△CEB;
（2）若△DEF的面积为2，求□ABCD的面积。
如图，已知∠A＝∠C，∠1＋∠2＝180°，试问：∠B与∠F有什么关系？为什么？
解：∠B＝∠F，理由如下：
∵∠A＝∠C
∴∥（）
∴∠BDC＝∠B（）
∵∠1＋∠2＝180°
且∠1＋∠3（）
∴∠3＋∠2＝180°
∴∥（）
∴∠BDC＝（）
∴∠B＝∠F（）
如图所示，某校一块长为2a米的正方形空地是七年级4个班的清洁区，其中分给七（1）班的清洁区是一块边长为
米的正方形，
。
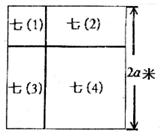
（1）分别求出七（2）、七（3）班的清洁区的面积；
（2）七（4）班的清洁区的面积比七（1）班的清洁区的面积多多少平方米？
已知∠1＝∠2＝∠3＝59°，求∠4的度数。
先化简，再求值：
，其中
计算
（1）
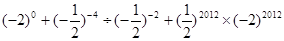
（2）