（本小题满分14分））
某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿场售价与上市时间的关系用图一的一条折线表示；西红柿的种植成本与上市时间的关系用图二的抛物线段表示。
（Ⅰ）写出图一表示的市场售价与时间的函数关系式
；写出图二表示的种植成本与上市时间的函数关系式
；
（Ⅱ）假如设定市场售价减去种植成本为纯收益，问何时上市的西红柿纯收益最大？（注：市场售价和种植成本的单位：元/102㎏，时间单位：天）
有A、B、C三个盒子，其中一个内放有一个苹果，在三个盒子上各有一张纸条.
A盒子上的纸条写的是“苹果在此盒内”，
B盒子上的纸条写的是“苹果不在此盒内”，
C盒子上的纸条写的是“苹果不在A盒内”.
如果三张纸条中只有一张写的是真的，请问苹果究竟在哪个盒子里？
写出下列各命题的否定及其否命题，并判断它们的真假.
（1）若x、y都是奇数，则x+y是偶数；
（2）若xy=0，则x=0或y=0；
（3）若一个数是质数，则这个数是奇数.
已知关于x的实系数二次方程x2+ax+b=0有两个实数根α、β，
证明:|α|<2且|β|<2是2|a|<4+b且|b|<4的充要条件.
已知数列{an}的前n项Sn=pn+q(p≠0,p≠1),求数列{an}是等比数列的充要条件.
已知p:|1－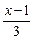
|≤2,q:x2－2x+1－m2≤0(m>0),若⌐p是⌐q的必要而不充分条件，求实数m的取值范围.