写出下列各命题的否定及其否命题,并判断它们的真假.
(1)若x、y都是奇数,则x+y是偶数;
(2)若xy=0,则x=0或y=0;
(3)若一个数是质数,则这个数是奇数.
(本小题满分1 3分)如图,在△ABC中,已知B= ,AC=4
,AC=4 ,D为BC边上一点.
,D为BC边上一点.
(I)若AD=2,S△ABC=2 ,求DC的长;
,求DC的长;
(Ⅱ)若AB=AD,试求△ADC的周长的最大值.
.(本小题满分13分)某学院为了调查本校学生201 1年9月“健康上网”(健康上网是指每天上网不超过两小时)的天数情况,随机抽取了40名本校学生作为样本,统计他们在该月30天内健康上网的天数,并将所得数据分成以下六组:[O,5],(5,1 O],…,(25,30],由此画出样本的频率分布直方图,如图所示.
(I)根据频率分布直方图,求这40名学生中健康上网天数超过20天的人数;
(Ⅱ)现从这40名学生中任取2名,设Y为取出的2名学生中健康上网天数超过20天的人数,求Y的分布列及其数学期望E(Y).
(本小题满分l 3分)在数列{an}中,a1=2,an+l=an+cn (n∈N*,常数c≠0),且a1,a2,a3成等比数列.
(I)求c的值;
(Ⅱ)求数列{an}的通项公式.
(本小题满分1 4分)已知m,t∈ R,函数f (x) ="(x" - t)3+m.
R,函数f (x) ="(x" - t)3+m.
(I)当t =1时,
(i)若f (1) =1,求函数f (x)的单调区间;
(ii)若关于x的不等式f (x)≥x3—1在区间[1,2]上有解,求m的取值范围;
(Ⅱ)已知曲线y= f (x)在其图象上的两点A(x1,f (x1)),B(x2,f (x2)))( x1≠x2)处的切线
分别为l1、l2.若直线l1与l2平行,试探究点A与点B的关系,并证明你的结论.
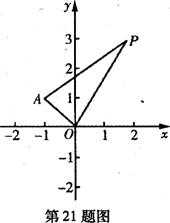
(本小题满分1 2分)在平面直角坐标系xOy中,已知点A(一1,1),P是动点,且三角形POA的三边所在直线的斜率满足kOP+kOA=kPA.
(I)求点P的轨迹C的方程;
(Ⅱ)若Q是轨迹C上异于点P的一个点,且 ,直线OP与QA交于点M,试探究:点M的横
,直线OP与QA交于点M,试探究:点M的横 坐标是否为定值?并说明理由.
坐标是否为定值?并说明理由.