(本小题满分12分)设函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且
(1)求函数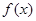 的解析式;
的解析式;
(2)若f(x)在[0,1)上为增函数,求不等式
 的解集
的解集
已知 ,
, ,圆
,圆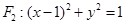 ,一动圆在
,一动圆在 轴右侧与
轴右侧与 轴相切,同时与圆
轴相切,同时与圆 相外切,此动圆的圆心轨迹为曲线C,曲线E是以
相外切,此动圆的圆心轨迹为曲线C,曲线E是以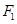 ,
, 为焦点的椭圆。
为焦点的椭圆。
(1)求曲线C的方程;
(2)设曲线C与曲线E相交于第一象限点P,且 ,求曲线E的标准方程;
,求曲线E的标准方程;
(3)在(1)、(2)的条件下,直线 与椭圆E相交于A,B两点,若AB的中点M在曲线C上,求直线
与椭圆E相交于A,B两点,若AB的中点M在曲线C上,求直线 的斜率
的斜率 的取值范围。
的取值范围。
有一批货物需要用汽车从生产商所在城市甲运至销售商所在城市乙,已知从城市甲到城市乙只有两条公路,且通过这两条公路所用的时间互不影响。
据调查统计,通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布如下表:
| 所用的时间(天数) |
10 |
11 |
12 |
13 |
| 通过公路1的频数 |
20 |
40 |
20 |
20 |
| 通过公路2的频数 |
10 |
40 |
40 |
10 |
假设汽车A只能在约定日期(某月某日)的前11天出发,汽车B只能在约定日期的前12天出发。
(1)为了尽最大可能在各自允许的时间内将货物运往城市乙,估计汽车A和汽车B应如何选择各自的路径;
(2)若通过公路1、公路2的“一次性费用”分别为3.2万元、1.6万元(其它费用忽略不计),此项费用由生产商承担。如果生产商恰能在约定日期当天将货物送到,则销售商一次性支付给生产商40万元,若在约定日期前送到,每提前一天销售商将多支付给生产商2万元;若在约定日期后送到,每迟到一天销售商将少支付给生产商2万元。如果汽车A、B长期按(1)所选路径运输货物,试比较哪辆汽车为生产商获得的毛利润更大。
(注:毛利润=(销售商支付给生产商的费用)—(一次性费用))
如图,在三棱柱ABC—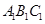 中,底面
中,底面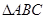 为正三角形,
为正三角形,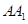
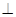 平面ABC,
平面ABC,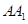 =2AB,N是
=2AB,N是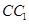 的中点,M是线段
的中点,M是线段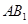 上的动点。
上的动点。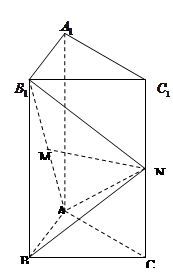
(1)当M在什么位置时,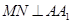 ,请给出证明;
,请给出证明;
(2)若直线MN与平面ABN所成角的大小为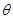 ,求
,求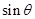 的最大值。
的最大值。
已知数列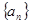 的前项和为
的前项和为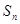 ,满足
,满足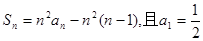 ,
,
(1)令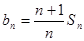 ,证明:
,证明: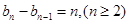 ;
;
(2)求数列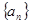 的通项公式。
的通项公式。
设对于任意实数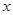 ,不等式
,不等式 恒成立.
恒成立.
(1)求 的取值范围;
的取值范围;
(2)当 取最大值时,解关于
取最大值时,解关于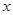 的不等式:
的不等式: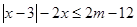 .
.