(本小题满分12分)(解答过程写在试卷上无效)
对于函数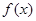 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称
,则称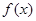 为“局部奇函数”.
为“局部奇函数”. 为定义在
为定义在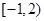 上的“局部奇函数”;
上的“局部奇函数”;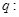 曲线
曲线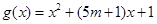 与
与 轴交于不同的两点;
轴交于不同的两点;
若 为假命题,
为假命题,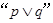 为真命题,求
为真命题,求 的取值范围.
的取值范围.
设数列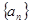 的前
的前 项和为
项和为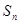 ,且满足
,且满足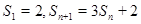
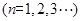 .
.
(Ⅰ)求证:数列 为等比数列;
为等比数列;
(Ⅱ)求通项公式 ;
;
(Ⅲ)若数列 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列 的前
的前 项和为
项和为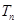 .
.
在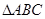 中,角
中,角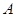 ,
, ,
,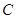 所对的边长分别是
所对的边长分别是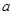 ,
,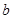 ,
, . 满足
. 满足 .
.
(Ⅰ)求角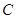 的大小;
的大小;
(Ⅱ)求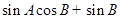 的最大值.
的最大值.
申请某种许可证,根据规定需要通过统一考试才能获得,且考试最多允许考四次. 设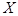 表示一位申请者经过考试的次数,据统计数据分析知
表示一位申请者经过考试的次数,据统计数据分析知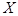 的概率分布如下:
的概率分布如下:
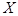 |
1 |
2 |
3 |
4 |
| P |
0.1 |
 |
0.3 |
0.1 |
(Ⅰ)求一位申请者所经过的平均考试次数;
(Ⅱ)已知每名申请者参加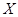 次考试需缴纳费用
次考试需缴纳费用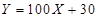 (单位:元),求两位申请者所需费用的和小于500元的概率;
(单位:元),求两位申请者所需费用的和小于500元的概率;
(Ⅲ)在(Ⅱ)的条件下, 4位申请者中获得许可证的考试费用低于300元的人数记为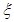 ,求
,求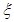 的分布列.
的分布列.
某班同学寒假期间在三个小区进行了一次有关“年夜饭在哪吃”的调查,若年夜饭在家吃的称为“传统族”,否则称为“前卫族”,这两类家庭总数占各自小区家庭总数的比例如下:
| A小区 |
传统族 |
前卫族 |
| 比例 |
 |
 |
| B小区 |
传统族 |
前卫族 |
| 比例 |
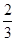 |
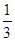 |
| C小区 |
传统族 |
前卫族 |
| 比例 |
 |
 |
(Ⅰ)从A , B , C三个小区中各选一个家庭,求恰好有2个家庭是“传统族”的概率(用比例作为相应的概率);
(Ⅱ)在C小区按上述比例选出的20户家庭中,任意抽取3户家庭,其中“前卫族”家庭的数量记为X,求X的分布列和期望 .
.
已知函数 (其中
(其中 ).
).
(Ⅰ)求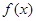 的单调区间;
的单调区间;
(Ⅱ)求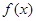 在
在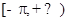 上的最大值与最小值.
上的最大值与最小值.