已知抛物线C:y2=4x,点M(m,0)在x轴的正半轴上,过点M的直线l与抛物线C相交于A,B两点,O为坐标原点.
(1)若m=1,且直线l的斜率为1,求以AB为直径的圆的方程;
(2)是否存在定点M,使得不论直线l绕点M如何转动, 恒为定值?
恒为定值?

设△ABC的内角A,B,C的对边分别为a,b,c,且A=60°,c=3b.求:
(1)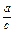 的值;
的值;
(2) 的值.
的值.
在△ABC中,设A、B、C的对边分别为a、b、c,向量m=(cosA,sinA),n=(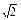 -sinA,cosA),若|m+n|=2.
-sinA,cosA),若|m+n|=2.
(1)求角A的大小;
(2)若b=4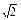 ,且c=
,且c=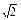 a,求△ABC的面积.
a,求△ABC的面积.
已知向量a=(cosx,sinx),|b|=1,且a与b满足|ka+b|=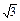 |a-kb| (k>0).
|a-kb| (k>0).
(1)试用k表示a·b,并求a·b的最小值;
(2)若0≤x≤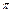 ,b=
,b=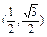 ,求a·b的最大值及相应的x值.
,求a·b的最大值及相应的x值.
设a=(-1,1),b=(4,3),c=(5,-2),
(1)求证a与b不共线,并求a与b的夹角的余弦值;
(2)求c在a方向上的投影;
(3)求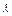 1和
1和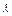 2,使c=
2,使c=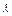 1a+
1a+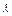 2b.
2b.
在海岸A处,发现北偏东45°方向,距离A( -1)n mile的B处有一艘走私船,在A处北偏西75°的方向,距离A 2 n mile的C处的缉私船奉命以10
-1)n mile的B处有一艘走私船,在A处北偏西75°的方向,距离A 2 n mile的C处的缉私船奉命以10 n mile/h的速度追截走私船.此时,走私船正以10 n mile/h的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?
n mile/h的速度追截走私船.此时,走私船正以10 n mile/h的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?