已知n次多项式f(x)=anxn+an-1xn-1+…+a1x+a0,用秦九韶算法求f(x0)的值,需要进行的乘法运算、加法运算的次数依次是( ).
| A.n,n | B.2n,n | C.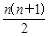 ,n ,n |
D.n+1,n+1 |
函数 在区间
在区间 上的最大值是()
上的最大值是()
A. |
B. |
C. |
D. |
已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是()
A. =1.23x+4 =1.23x+4 |
B. ="1.23x+5" ="1.23x+5" |
C. =1.23x+0.08 =1.23x+0.08 |
D. =0.08x+1.23 =0.08x+1.23 |
下面的流程图,求输出的 y 的表达式是()
A. |
B. |
C. |
D. |
条件 “
“ ”,条件
”,条件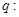 “
“ ”,则
”,则 是
是 的()
的()
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
函数y=x2cosx的导数为()
| A.y′=x2cosx-2xsinx | B.y′=2xcosx+x2sinx |
| C.y′=2xcosx-x2sinx | D.y′=xcosx-x2sinx |