如图所示，光滑绝缘的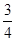
圆形轨道BCDG位于竖直平面内，轨道半径为R，下端与水平绝缘轨道在B点平滑连接，整个轨道处在水平向左的匀强电场中．现有一质量为m、带正电的小滑块（可视为质点）置于水平轨道上，滑块受到的电场力大小为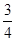mg，滑块与水平轨道间的动摩擦因数为0.5，重力加速度为g．求：
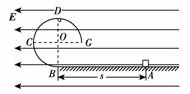
（1）若滑块从水平轨道上距离B点为s＝3R的A点由静止释放，求滑块到达与圆心O等高的C点时的速度大小；
（2）在（1）的情况下，求滑块到达C点时对轨道的作用力大小；
（3）改变s的大小，使滑块恰好始终沿轨道滑行，且从G点飞出轨道，求滑块在圆轨道上滑行过程中的最小速度大小．
“蹦极”是一项勇敢者的运动，如图所示，某人用弹性橡皮绳拴住身体从高空P处自由下落，在空中感受失重的滋味。若此人质量为50
，橡皮绳长20m，人可看成质点，且此人从P点自静止下落到最低点所用时间为6s （g = 10
）。求：
（1）此人下落到橡皮绳刚伸直（无伸长）时，人的动量是多少?
（2）从橡皮绳开始拉伸到人下落到最低点的过程中橡皮绳对人的平均作用力为多大?
如图所示，质量为m＝1kg的可视为质点的小物块轻轻放在水平匀速运动的传送带上的P点，随传送带运动到A点后水平抛出，小物块恰好无碰撞的沿圆弧切线从B点进入竖直光滑圆弧轨道下滑，圆弧轨道与质量为M＝2kg的足够长的小车左端在最低点O点相切，并在O点滑上小车，水平地面光滑，当物块运动到障碍物Q处时与Q发生无机械能损失的碰撞。碰撞前物块和小车已经相对静止，而小车可继续向右运动（物块始终在小车上），小车运动过程中和圆弧无相互作用。已知圆弧半径R＝1.0m，圆弧对应的圆心角θ为53°，A点距水平面的高度h＝0.8m，物块与小车间的动摩擦因数为μ＝0.1，重力加速度g＝10m/s2，sin53°＝0.8，cos53°＝0.6。试求：
（1）小物块离开A点的水平初速度v1；
（2）小物块经过O点时对轨道的压力；
（3）第一次碰撞后直至静止，物块相对小车的位移和小车做匀减速运动的总时间。
2012年6月16日，“神舟九号”宇宙飞船搭载3名航天员飞天，并于6月18日14∶00与“天宫一号”成功对接。在发射时，“神舟九号”宇宙飞船首先要发射到离地面很近的圆轨道，然后经过多次变轨后，最终与在距地面高度为h的圆形轨道上绕地球飞行的“天宫一号”完成对接，之后，整体保持在距地面高度仍为h的圆形轨道上绕地球继续运行．已知地球半径为R，地面附近的重力加速度为g。求：
（1）地球的第一宇宙速度；
（2）“神舟九号”宇宙飞船在近地圆轨道运行的速度与对接后整体的运行速度之比。
如图甲所示，有一足够长的粗糙斜面，倾角θ＝37°，一滑块以初速度v0＝16m/s从底端A点滑上斜面，滑至B点后又返回到A点．滑块运动的图象如图乙所示，求：（已知：sin37°＝0.6，cos37°＝0.8，重力加速度g＝10m/s2）
（1）AB之间的距离；
（2）滑块再次回到A点时的速度。
两个相同的小球A和B，质量均为m，用长度相同的两根细线把A、B两球悬挂在水平天花板上的同一点O，并用长度相同的细线连接A、B两小球，然后，用一水平方向的力F作用在小球A上，此时三根细线均处于直线状态，且OB细线恰好处于竖直方向，如图所示。如果不考虑小球的大小，两小球均处于静止状态，则：
（1）OB绳对小球的拉力为多大？
（2）OA绳对小球的拉力为多大？
（3）作用力F为多大？