2013年6月，我国成功实现目标飞行器“神舟十号”与轨道空间站“天宫一号”的对接．如图所示，已知“神舟十号”从捕获“天宫一号”到实现对接用时t，这段时间内组合体绕地球转过的角度为θ（此过程轨道不变，速度大小不变），地球半径为R，地球表面重力加速度为g，万有引力恒量G，不考虑地球自转；求：
（1）地球质量M；
（2）组合体运动的周期T；
（3）组合体所在圆轨道离地高度H。
一圆柱形汽缸，
内部截面积为S，其活塞可在汽缸内无摩擦地滑动，汽缸内密封有理想气体，外部大气压强为p0，当汽缸卧放在水平面上时，活塞距缸底为L0，如图所示．当汽缸竖直放置开口向上时，活塞距缸底为4/5L0.求活塞的质量
电灯泡内充有氦氩混合气体，如果要使电灯泡内的混合气体在500℃时的压强不超过一个大气压，则在20℃的室温下充气，电灯泡内气体压强至多能充到多少个大气压？
如图，一个玻璃管竖直放置，开口向上，一小段水银柱封闭一定质量的空气，23℃时空气之长60cm，外界大气压始终保持1atm不变，问，当温度降低到0℃时，空气柱长度为多少？ 
真空中有一个电场，电场线如图所示.在这个电场中的A点放入电量为5.0×10-9C的点电荷，它受到的电场力为3.0×10-4N.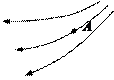
(1)画出A点电场强度的方向.
(2)求出A点电场强度的大小.
(3)若把该点电荷从电场中移走, 则A点电场强度是多大.
一根长为0.20m的
直导线，垂直于某匀强磁场方向放置，当导线中通有1A的电流时，导线受到的安培力大小为0.08N，
则：
（1）磁场的磁感应强度为多大？
（2）当导线中的电流增大为2A时，导线受到的安培力为多大？