(本小题满分12分)已知圆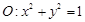 和定点
和定点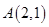 ,由圆
,由圆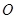 外一点
外一点 向圆
向圆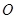 引切线
引切线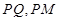 ,切点为
,切点为 ,且满足
,且满足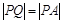 .
.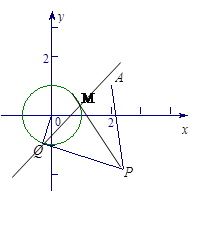
(1)求实数 间满足的等量关系;
间满足的等量关系;
(2)若以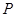 为圆心的圆
为圆心的圆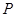 与圆
与圆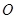 有公共点,试求圆
有公共点,试求圆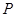 的半径最小时圆
的半径最小时圆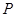 的方程;
的方程;
(3)当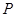 点的位置发生变化时,直线
点的位置发生变化时,直线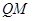 是否过定点,如果是,求出定点坐标,如果不是,说明理由.
是否过定点,如果是,求出定点坐标,如果不是,说明理由.
(本小题满分10分)选修4—5:不等式选讲
已知函数

(1)当 时,求不等式
时,求不等式 的解集;
的解集;
(2)若不等式 对任意实数
对任意实数 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分10分)选修4—1:几何证明选讲
如图,四边形ACED是圆内接四边形,延长AD与CE的延长线交于点B,且AD=DE,AB=2AC.
(Ⅰ)求证:BE=2AD;
(Ⅱ)当AC=2,BC=4时,求AD的长.
(本小题满分12分)已知函数
(1)求函数f(x)的单调递增区间;
(2)若在区间[1,e]上至少存在一点 成立,求实数p的取值范围.
成立,求实数p的取值范围.
设数列 的前
的前 项和为
项和为 ,点
,点 在直线
在直线 上.
上.
(1)求数列 的通项公式;
的通项公式;
(2)在 与
与 之间插入
之间插入 个数,使这
个数,使这 个数组成公差为
个数组成公差为 的等差数列,求数列
的等差数列,求数列 的前
的前 项和
项和 .
.
已知直线l:y=kx+1,圆C:(x-1)2+(y+1)2=12.
(1)试证明:不论k为何实数,直线l和圆C总有两个交点;
(2)求直线l被圆C截得的最短弦长.