德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数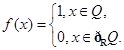
被称为狄利克雷函数,其中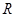 为实数集,
为实数集,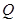 为有理数集,则关于函数
为有理数集,则关于函数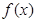 有如下四个命题:①
有如下四个命题:①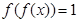 ;②函数
;②函数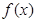 是偶函数;③任取一个不为零的有理数
是偶函数;③任取一个不为零的有理数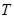 ,
,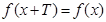 对任意的
对任意的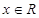 恒成立;④存在三个点
恒成立;④存在三个点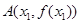 ,
,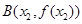 ,
,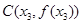 ,使得△
,使得△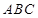 为等边三角形.其中真命题的个数为()
为等边三角形.其中真命题的个数为()
| A.1 | B.2 | C.3 | D.4 |
若 ,则
,则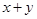 的最小值是()
的最小值是()
| A.8 | B.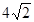 |
C.4 | D.2 |
如图所示的是函数 和函数
和函数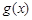 的部分图象,则函数
的部分图象,则函数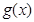 的解析式是()
的解析式是()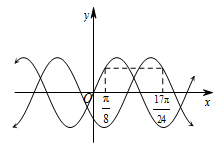
A.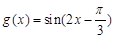 |
B.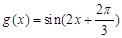 |
C.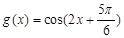 |
D.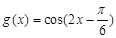 |
下列命题中错误的是 ()
A.如果平面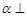 平面 平面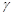 ,平面 ,平面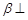 平面 平面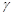 , ,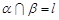 ,那么 ,那么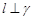 |
B.如果平面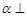 平面 平面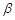 ,那么平面 ,那么平面 内一定存在直线平行于平面 内一定存在直线平行于平面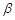 |
C.如果平面 不垂直于平面 不垂直于平面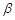 ,那么平面 ,那么平面 内一定不存在直线垂直于平面 内一定不存在直线垂直于平面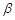 |
D.如果平面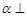 平面 平面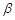 ,过 ,过 内任意一点作交线的垂线,那么此垂线必垂直于 内任意一点作交线的垂线,那么此垂线必垂直于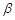 |
已知 为实数,则“
为实数,则“ ”是“
”是“ 且
且 ”的()
”的()
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |