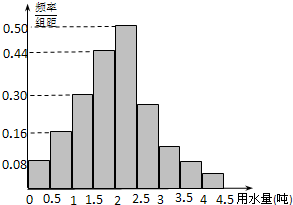
（本小题满分10分）某地区100位居民的人均月用水量（单位：-优题课

题文

（本小题满分10分）某地区100位居民的人均月用水量（单位：t）的频率分布直方图及频数分布表如下：

分组	频数
[0，0．5）	4
[0．5，1）	8
[1，1．5）	15
[1．5，2）	22
[2，2．5）	25
[2．5，3）	14
[3，3．5）	6
[3．5，4）	4
[4，4．5]	2
合计	100

（1）根据频率分布直方图估计这组数据的众数与平均数；
（2）当地政府制定了人均月用水量为3t的标准，若超出标准加倍收费，当地政府解释说，85%以上的居民不超出这个标准，这个解释对吗？为什么？

科目数学题型解答题难度较易

知识点：误差估计

登录免费查看答案和解析

相关试题

如图，长方形物体E在雨中沿面 $P$ （面积为 $S$ ）的垂直方向作匀速移动，速度为 $v (v > 0)$ ，雨速沿E移动方向的分速度为 $c (c \in R)$ .E移动时单位时间内的淋雨量包括两部分：（1） $P$ 或 $P$ 的平行面（只有一个面淋雨）的淋雨量，假设其值与 $|v - c| \times S$ 成正比，比例系数为 $\frac{1}{10}$ ；（2）其它面的淋雨量之和，其值为 $\frac{1}{2}$ ，记 $y$ 为 $E$ 移动过程中的总淋雨量，当移动距离 $d = 100$ ，面积 $S = \frac{3}{2}$ 时.

（1）写出 $y$ 的表达式
（2）设 $0 < v \leq 10, 0 < c \leq 5$ ，试根据 $c$ 的不同取值范围，确定移动速度 $v$ ，使总淋雨量 $y$ 最少.

如图，在圆锥 $P O$ 中,已知 $P O = \sqrt{2}, ⊙ O$ 的直径 $A B = 2, C$ 是 $\overset{⏜}{A B}$ 的中点, $D$ 为 $A C$ 的中点.

（1）证明：平面 $P O D ⊥$ 平面 $P A C$

（2）求二面角 $B - P A - C$ 的余弦值．

某商店试销某种商品20天，获得如下数据：

日销售量（件）	0	1	2	3
频数	1	5	9	5

试销结束后（假设该商品的日销售量的分布规律不变），设某天开始营业时有该商品3件，当天营业结束后检查存货，若发现存货少于2件，则当天进货补充至3件，否则不进货，将频率视为概率。
（1）求当天商品不进货的概率；
（2）记 $X$ 为第二天开始营业时该商品的件数，求 $X$ 的分布列和数学期望。

在 $△ A B C$ 中，角 $A, B, C$ 所对的边分别为 $a, b, c$ ，且满足 $c \sin A = a \cos C$ .
（1）求角 $C$ 的大小；
（2）求 $\sqrt{3} \sin A - \cos (B + \frac{π}{4})$ 的最大值，并求取得最大值时角 $A, B$ 的大小．

已知函数(a是常数，a∈R)
（1）当a=1时求不等式的解集．
（2）如果函数恰有两个不同的零点，求a的取值范围．

试卷网试题网古诗词网作文网范文网