如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点, M为CD的中点.
M为CD的中点.
(Ⅰ)求点M的轨迹方程;
(Ⅱ)过M作AB的垂线,垂足为N,若存在正常数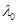 ,使
,使 ,且P点到A、B 的距离和为定值,求点P的轨迹E的方程;
,且P点到A、B 的距离和为定值,求点P的轨迹E的方程;
(Ⅲ)过 的直线与轨迹E交于P、Q两点,求
的直线与轨迹E交于P、Q两点,求 面积的最大值.
面积的最大值.
(本小题满分16分)已知常数 ,函数
,函数
(1)求 的单调递增区间;
的单调递增区间;
(2)若 ,求
,求 在区间
在区间 上的最小值
上的最小值 ;
;
(3)是否存在常数 ,使对于任意
,使对于任意 时,
时, 恒成立,若存在,求出
恒成立,若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。
(本小题满分16分)已知在直角坐标系中, ,其中数列
,其中数列 都是递增数列。
都是递增数列。
(1)若 ,判断直线
,判断直线 与
与 是否平行;
是否平行;
(2)若数列 都是正项等差数列,设四边形
都是正项等差数列,设四边形 的面积为
的面积为 .
.
求证: 也是等差数列;
也是等差数列;
(3)若 ,
, ,记直线
,记直线 的斜率为
的斜率为 ,数列
,数列 前8项依次递减,求满足条件的数列
前8项依次递减,求满足条件的数列 的个数。
的个数。
(本小题满分16分)如图,在直角坐标系中, 三点在
三点在 轴上,原点
轴上,原点 和点
和点 分别是线段
分别是线段 和
和 的中点,已知
的中点,已知 (
( 为常数),平面上的点
为常数),平面上的点 满
满 。
。
(1)试求点 的轨迹
的轨迹 的方程;
的方程;
(2)若点 在曲线
在曲线 上,求证:点
上,求证:点 一定在某圆
一定在某圆 上;
上;
(3)过点 作直线
作直线 ,与圆
,与圆 相交于
相交于 两点,若点
两点,若点 恰好是线段
恰好是线段 的中点,试求直线
的中点,试求直线 的方程。
的方程。
(本小题满分14分)某地区的农产品 第
第 天
天 的销售价格
的销售价格 (元∕百斤),一农户在第
(元∕百斤),一农户在第 天
天 农产品
农产品 的销售量
的销售量 (百斤)。
(百斤)。
(1)求该农户在第7天销售农产品 的收入;
的收入;
(2)问这20天中该农户在哪一天的销售收入最大?
(本小题满分14分)已知 ,
, ,
, 。
。
(1)若 ,记
,记 ,求
,求 的值;
的值;
(2)若 ,
, ,且
,且 ∥
∥ ,求证:
,求证: 。
。