(.重庆市B卷,第22题,10分)某校七年级(1)班班主任对本班学生进行了“我最喜欢的课外活动”的调查,并将调查结果分为书法和绘画类(记为
| A.音乐类(记为 | B.球类(记为 | C.其他类(记为 | D.根据调查结果发现该班每个学生都进行了等级且只登记了一种自己最喜欢的课外活动.班主任根据调查情况把学生都进行了归类,并制作了如下两幅统计图,请你结合图中所给信息解答下列问题: |

(1)七年级(1)班学生总人数为_______人,扇形统计图中D类所对应扇形的圆心角为_____度,请补全条形统计图;
(2)学校将举行书法和绘画比赛,每班需派两名学生参加,A类4名学生中有两名学生擅长书法,另两名擅长绘画.班主任现从A类4名学生中随机抽取两名学生参加比赛,请你用列表或画树状图的方法求出抽到的两名学生恰好是一名擅长书法,另一名擅长绘画的概率.
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
⑴求证:CE=CF;
⑵若G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
如图,在矩形ABCD中,AB=16cm,AD=6cm,动点P、Q分别从A、C同时出发,点P以每秒3cm的速度向B移动,一直达到B止,点Q以每秒2cm的速度向D移动.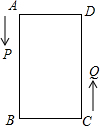
(1)P、Q两点出发后多少秒时,四边形PBCQ的面积为36cm2;
(2)是否存在某一时刻,使PBCQ为正方形?
如图,已知:在ΔABC中,AB=AC,AD⊥BC,垂足为D,AN是ΔABC外角∠CAM的平分线,CE⊥AN,垂足为E.求证:四边形ADCE是矩形.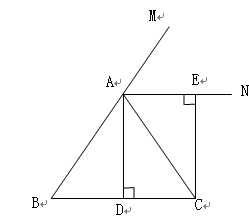
某商场购进一种单价为40元的篮球,如果以单价50元出售,那么每月可售出500个,根据销售经验,售价每提高1元,销售量相应减少10个。如果每月销售这种篮球的利润是8000元,又能让顾客得到实惠,篮球的售价应定为多少元?
在下面指定位置画出此实物图的三种视图.
