（本小题满分13分）如图，椭圆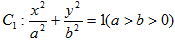
的离心率为
，
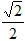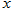轴被曲线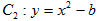
截得的线段长等于
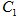的短轴长．
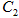与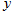
轴的交点为M，过坐标原点O的直线
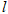与相交于点A、B．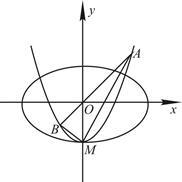
（1）求，的方程；
（2）求证：MA⊥MB．
（本小题满分12分）
设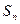
是正项数列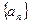
的前n项和且
.
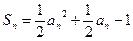（1）求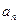
； （2）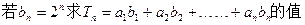
（本小题满分12分）
如图，直二面角D—AB—E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE.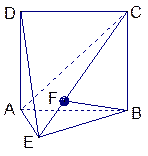
（Ⅰ）求证AE⊥平面BCE；
（Ⅱ）求二面角B—AC—E的大小；
（本小题满分12分）
甲、乙两人在罚球线投球命中的概率分别为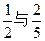
，投中得1分，投不中得0分.
（Ⅰ）甲、乙两人在罚球线各投球一次，求两人得分之和ξ的数学期望；
（Ⅱ）甲、乙两人在罚球线各投球二次，求这四次投球中至少一次命中的概率；
（本小题满分10分）已知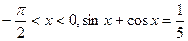
.
（I）求sinx－cosx的值；
（Ⅱ）求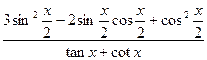
的值.
（本
小题14分）已知函数
的图像与函数
的图像关于点
对称
（1）求函数的解析式；
（2）若
，
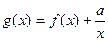在区间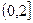
上的值不小于6，求实数a的取值范围．