如图,在直四棱柱ABCD﹣A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC, AB∥DC.

(1)求证:D1C⊥AC1;
(2)设E是DC上一点,试确定E的位置,使D1E∥平面A1BD,并说明理由.
(8分)如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:
(1) FD∥平面ABC;
(2) AF⊥平面EDB.
(本小题满分8分)对于函数 ,若存在实数
,若存在实数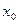 ,使
,使 =
=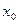 成立,则称
成立,则称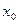 为
为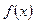 的不动点.
的不动点.
⑴当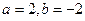 时,求
时,求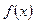 的不动点;
的不动点;
⑵若对于任意实数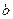 ,函数
,函数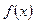 恒有两个不相同的不动点,求
恒有两个不相同的不动点,求 的取值范围.
的取值范围.
(本小题满分8分)A、B两城相距100km,在两地之间距A城xkm处D地建一核电站给A、B两城供电,为保证城市安全.核电站距市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数 .若A城供电量为20亿度/月,B城为10亿度/月.
.若A城供电量为20亿度/月,B城为10亿度/月.
(Ⅰ)把月供电总费用y表示成x的函数,并求定义域;
(Ⅱ)核电站建在距A城多远,才能使供电费用最小.
(本小题满分6分)
按要求完成下列各题:
⑴求函数 的定义域;
的定义域;
⑵当 时,证明函数
时,证明函数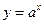 在
在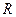 上是减函数.
上是减函数.
(本小题满分8分)
⑴已知△ABC三个顶点的坐标分别为A(4,1),B(0,3),C(2,4),边AC的中点为D,求AC边上中线BD所在的直线方程并化为一般式;
⑵已知圆C的圆心是直线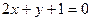 和
和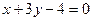 的交点上且与直线
的交点上且与直线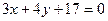 相切,求圆C的方程.
相切,求圆C的方程.