（.重庆市A卷，第25题，12分）如图1，在△ABC中，
ACB=90°，BAC=60°，点E是∠BAC角平分线上一点，过点E作AE的垂线，过点A作AB的线段，两垂线交于点D，连接DB，点F是BD的中点.DH⊥AC，垂足为H，连接EF，HF。
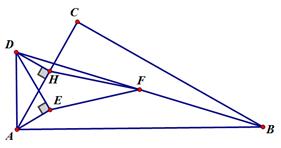
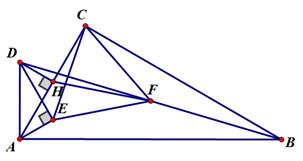
2图1 图2
（1）如图1，若点H是AC的中点，AC=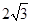
，求AB，BD的长。
（2）如图1，求证：HF=EF。
（3）如图2，连接CF，CE，猜想：△CEF是否是等边三角形？若是，请证明；若不是，请说明理由。
．如图，在△ABC中，点E在AB上，点D在BC上，BD=BE，∠BAD=∠BCE，AD与CE相交于点F，试判断△AFC的形状，并说明理由．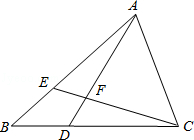
如图所示，一根旗杆升旗的绳垂直落地后还剩余1米，若将绳子拉直，则绳端离旗杆底端的距离（BC）有5米．求旗杆的高度．
如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
（1）在图中画出与△ABC关于直线l成轴对称的△A′B′C′；
（2）在直线l上找一点P（在答题纸上图中标出），使PB+PC
的长最短，这个最短长度是 ．
(本题满分
分)已知
和
互为相反数，求x+4y的平方根。
(本题满分
分)求下面各式中的
：
（1）
（2）