天文学家将相距较近,仅在彼此的引力作用填运行的两颗恒星称为双星,双星系统在银河系中很普遍,利用双星系统中两颗恒星的运动特征可推算出它们的总质量,已知某双星系统中两颗恒星围绕它们连线上的某一点分别做匀速圆周运动,周期均为T,两颗恒星之间的距离为r,万有引力常量为G,试推算这个双星系统的总质量
中国四川消息:2008年5月12日14时28分,四川汶川地区发生了8.0级大地震,它是由两块断层受到挤压,造成剧烈上升及平行移位而造成的。已知地震波分为三种:纵波(P波),速度vP=9.9 km/s;横波(S波),速度vS=4.5 km/s;面波(L波),速度vL<vS,在浅源地震中破坏力最大。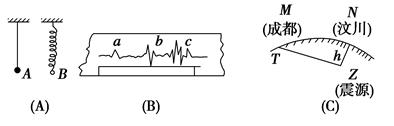
(1)位于震源上方的汶川地区某中学实验室内有水平摆A与竖直摆B,如图7-8(A)所示,地震发生时最先剧烈振动的是哪个摆?
(2)成都市地震观测台记录到的地震曲线假若如图7-8(B)所示,则由图可知a、b、c三处波形各对应于哪种地震波?若在曲线图上测得P波与S波的时间差为12.6 s,则地震台距震源多远?
(3)假若地震P波沿直线传播到成都市时,当地地表某标志物振动方向沿如图7-8(C)中ZT方向,测得某时刻该标志物的水平分位移x=23.1 mm,竖直分位移y=0.4 mm,试由此估算震源深度h。
2010年4月14日,青海省玉树县发生里氏7.1级大地震,已知地震中的纵波和横波在地表附近的传播速度为9.1 km/s和3.7 km/s,在某地观测站中,记录了玉树地震的纵波和横波到达该地的时间差为5.4 s。
(1)求这个观测站距玉树的距离。
(2)观测站首先观察到的是上下振动还是左右晃动?
如图7-6所示是一列向右传播的横波,请标出这列波中a、b、c、d…h等质点这一时刻的速度方向。
图7-6
汽车在一条起伏不平的公路上行驶,路面上凸起处相隔距离大约都是16 cm,汽车车身装在弹簧上,当汽车以8 m/s的速度行驶时,车身起伏振动得最剧烈.则弹簧固有频率是多少?
秒摆摆球质量为0.2 kg,它振动到最大位移时距最低点的高度为0.4 cm,当它完成10次全振动回到最大位移时,因有阻尼作用距最低点的高度变为0.3 cm.如果每振动10次给它补充一次能量,使摆球回到原高度,那么1 min内总共应补充多少能量?