一个有一定厚度的圆盘，可以绕通过中心垂直于盘面的水平轴转动，圆盘加速转动时，角速度的增加量Δω与对应之间Δt的比值定义为角加速度β（即
）．我们用电磁打点计时器、米尺、游标卡尺、纸带、复写纸来完成下述实验：（打点计时器所接交流电的频率为50Hz，A、B、C、D……为计数点，相邻两计数点间有四个点未画出）
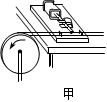
①如图甲所示，将打点计时器固定在桌面上，将纸带的一端穿过打点计时器的限位孔，然后固定在圆盘的侧面，当圆盘转动时，纸带可以卷在圆盘侧面上；
②接通电源，打点计时器开始打点，启动控制装置使圆盘匀加速转动；
③经过一段时间，停止转动和打点，取下纸带，进行测量．
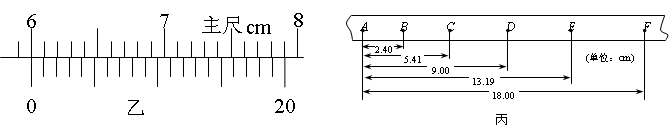
（1）用20分度的游标卡尺测得圆盘的半径如图乙所示，圆盘的半径r为 cm；
（2）由图丙可知，打下计数点D时，圆盘转动的角速度为 rad/s；（结果保留两位有效数字）
（3）纸带运动的加速度大小为 m/s2，圆盘转动的角加速度大小为 rad/s2。（结果保留两位有效数字）
在做《验证力的平行四边形定则》实验时.将橡皮筋的一端固定在A点,另一端拴上两根细绳,每根细绳分别连着一个量程为5N、最小刻度为0.1N的弹簧测力计.沿着两个不同的方向拉弹簧测力计.当橡皮筋的活动端拉到O点时,两根细绳相互垂直,如图所示.这时弹簧测力计的读数可从图中读出.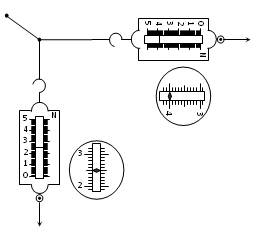
（1）由图可读得两个相互垂直的拉力的大小分别为______N和______N(只须读到0.1N).
（2）在本题的虚线方格纸上按作图法的要求画出这两个力及它们的合力.
某同学在做“探究小车速度随时间变化的规律”实验时，得到了如图一条较为理想的纸带，从某点开始，已在纸带上每隔0.1s取好一个计数点，即两计数点之间的时间间隔为0.1 s，依打点先后编为A、B、C、D如图所示，测出AB=1.2cm，AC=3.6cm，AD=7.2cm，则小车运动的加速度a=__________m/s2，打B点时小车的瞬时速度vB=__________m/s。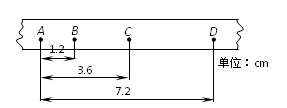
在“验证机械能守恒定律”的实验中，已知打点计时器所用电源的频率为50Hz。查得当地的重力加速度g＝9.80m/s2。测得所用的重物的质量为1.00kg。实验中得到一条点迹清晰的纸带，把第一个点记
作0，另选连续的4个点A
、B、C、D作为测量的点。经测量知道A、B、C、D各点到0点的距离分别为62.99cm、70.18 cm、77.76 cm、85.73 cm。根据以上数据，可知重物由0点运动到C点，重力势能的减少量等于J，动能的增加量等于J(取3位有效数字)。
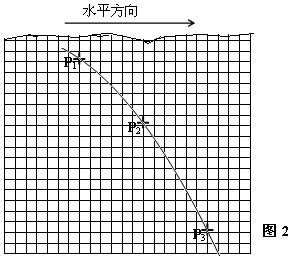
某同学得用图1所示装置做“研究平抛运动”的实验，根据实验结果在坐标纸上描出了小球水平抛出后的运动轨迹，但不慎将画有轨迹图线的坐标纸丢失了一部分，剩余部分如图2所示，图2中水平方向与竖直方向每小格的长度均代表0.10m，P1、P2和P3是轨迹图线上的3个点，P1和P2、P2和P3之间的水平距离相等。
完成下列填空：（重力加速度取9.8m/s2）
（1）设P1、P2、和P3的横坐标分别为x1、x2和x3，纵坐标分别为y1、y2和y3，从图2中可读出︱y1－ y2︱=_________m，︱y1－ y3︱=___
_______m，︱x1－ x2︱=__________m（保留两位小数）。
（2）若已测知抛出后小球在水平方向做匀速运动，利用（1）中读取的数据，求小球从P1运动到P2所用的时间
为___________s，小球抛出后的水平速度为___________m/s（均可用根号表示）。
如图所示装置，密闭容器Q和U型玻璃管a，竖直长玻璃管b通过橡皮管连接，玻璃管内装有水，将容器内的空气和外界隔离开。某同学利用此装置和温度计测量高山顶处的大气压强。实验步骤如下：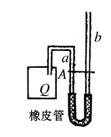
a．在山底处，调节竖直管b的高低位置，使得a、b管内水面相平，并在a的管上作出水面的标记A；
b．记录山底处的大气压强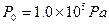
，并测量出山底处的温度T0；
c．将装置移到山顶处，调节竖直管b的高低位置，使得a管中的水面再次与标记A相平，测量b管的水面高出标记A处水面的高度h；
d．认为高山顶处的大气压P=P0－ρgh，其中g为重力加速度的值ρ为水的密度。
试说明上述测量步聚中漏掉或有错误的步聚，并加改正。
（1）漏掉的步骤是:
（2）错误的步骤是: （填序号），应改为：