如图甲所示，质量为m＝1kg的物体置于倾角为θ＝37°的固定且足够长的斜面上，对物体施以平行于斜面向上的拉力F，t1＝0.5s时撤去拉力，物体速度与时间（v-t）的部分图像如图乙所示。（g=10m/s2，sin37°＝0.6，cos37°＝0.8）问：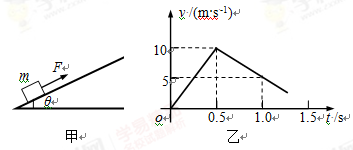
（1）物体与斜面间的动摩擦因数μ为多少？
（2）拉力F的大小为多少？
（3）物体沿斜面向上滑行的最大距离s为多少？
在游乐场中，有一种大型游戏机叫“跳楼机”.参加游戏的游客被安全带固定在座椅上，由电动机将座椅沿光滑的竖直轨道提升到离地面40m高处，然后由静止释放.为研究方便，可以认为座椅沿轨道做自由落体运动1.2 s后，开始受到恒定阻力而立即做匀减速运动，且下落到离地面4m高处时速度刚好减小到零．然后再让座椅以相当缓慢的速度稳稳下落，将游客送回地面.(取g=10m／s2)
求：（1）座椅在自由下落结束时刻的速度是多大?
（2）座椅在匀减速阶段的时间是多少？
（3）在匀减速阶段，座椅对游客的作用力大小是游客体重的多少倍?
如图甲所示，固定光滑细杆与水平地面成一定倾角，在杆上套有一个光滑小环，小环在沿杆方向向上的推力
作用下向上运动。0～2s内推力的大小为5.0N,2～4s内推力的大小变为5.5N，小环运动的速度随时间变化的规律如图乙所示，重力加速度
取10m/s2。求：
(1)小环在加速运动时的加速度
的大小；
(2)小环的质量
；
(3)细杆与水平地面之间的夹角
。
如图所示，半径为R，重为G的均匀球靠竖直墙放置，左下有厚为h的木块，若不计摩擦，用至少多大的水平推力F推木块才能使球离开地面？
如图甲所示是游乐场中过山车的实物图片，图乙是由它抽象出来的理想化模型（圆形轨道与斜轨道之间平滑连接，不计摩擦和空气阻力）。已知圆轨道的半径为R，质量为m的小车（视作质点）从P点由静止沿斜轨道下滑，进入圆轨道后沿圆轨道运动。已知P点到圆轨道最低点B的高度差H＝3R，通过计算说明小车能否顺利通过最高点A。若能顺利通过，小车在A点受到的压力有多大？
如图所示为中国月球探测工程的标志，它以中国书法的笔触，勾勒出一轮明月和一双踏在其上的脚印，象征着月球探测的终极梦想。一位勤于思考的同学，为探月宇航员设计了如下实验：在距月球表面高h处以初速度v0水平抛出一个物体，然后测量出该平抛物体的水平位移为x．通过查阅资料知道月球的半径为R，引力常量为G，若物体只受月球引力的作用，请你求出：（1）月球表面的重力加速度；（2）月球的质量；（3）环绕月球表面飞行的宇宙飞船的速率是多少。