(本小题10分)
如图,某建筑物BC顶部有一旗杆AB,且点A,B,C在同一直线上. 小红在D处观测旗杆顶部A的仰角为47°,观测旗杆底部B的仰角为42°. 已知点D到地面的距离DE为1.56m,EC =21m,求旗杆AB的高度和建筑物BC的高度(结果保留小数点后一位).参考数据:tan47°≈1.07,tan42°≈0.90.
如图,在平面直角坐标系xOy中,已知正比例函数 与一次函数
与一次函数 的图像交于点A.
的图像交于点A.
(1)求点A的坐标;
(2)设 轴上一点P(
轴上一点P( ,0),过点P作
,0),过点P作 轴的垂线(垂线位于点A的右侧),分别交
轴的垂线(垂线位于点A的右侧),分别交 和
和 的图像于点B、C,连接OC,若BC=
的图像于点B、C,连接OC,若BC= OA,求△OBC的面积.
OA,求△OBC的面积.
一次函数y= x的图像如图所示,它与二次函数y=ax2-4ax+c的图像交于A、B两点(其中点A在点B的左侧),与这个二次函数图像的对称轴交于点C.
x的图像如图所示,它与二次函数y=ax2-4ax+c的图像交于A、B两点(其中点A在点B的左侧),与这个二次函数图像的对称轴交于点C.
(1)求点C的坐标;
(2)设二次函数图像的顶点为D.
①若点D与点C关于x轴对称,且△ACD的面积等于3,求此二次函数的关系式;
②若CD=AC,且△ACD的面积等于10,求此二次函数的关系式.
已知二次函数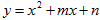 的图像经过点
的图像经过点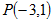 ,对称轴是经过
,对称轴是经过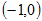 且平行于
且平行于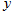 轴的直线。
轴的直线。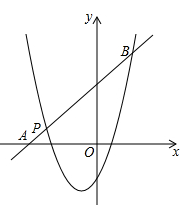
(1)求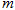 、
、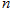 的值
的值
(2)如图,一次函数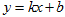 的图像经过点
的图像经过点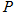 ,与
,与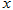 轴相交于点
轴相交于点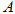 ,与二次函数的图像相交于另一点B,点B在点P的右侧,
,与二次函数的图像相交于另一点B,点B在点P的右侧,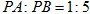 , 求一次函数的表达式。
, 求一次函数的表达式。
已知如图,在平面直角坐标系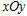 中,直线
中,直线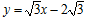 与
与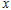 轴、
轴、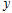 轴分别交于A,B两点,P是直线AB上一动点,⊙
轴分别交于A,B两点,P是直线AB上一动点,⊙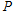 的半径为1.
的半径为1.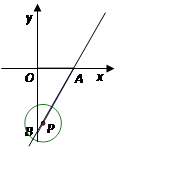
(1)判断原点O与⊙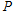 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当⊙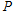 过点B时,求⊙
过点B时,求⊙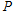 被
被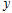 轴所截得的劣弧的长;
轴所截得的劣弧的长;
(3)当⊙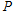 与
与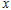 轴相切时,求出切点的坐标.
轴相切时,求出切点的坐标.
如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.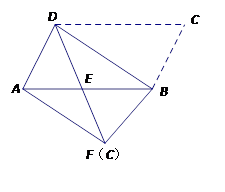
(1)求证: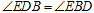 ;
;
(2)判断AF与BD是否平行,并说明理由.