在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r.则称P′为点P关于⊙C的反称点,下图为点P及其关于⊙C的反称点P′的示意图.
特别地,当点P′与圆心C重合时,规定CP′=0.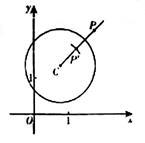
(1)当⊙O的半径为1时.
①分別判断点M(2,1),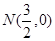 ,
,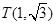 关于⊙O的反称点是否存在?若存在,求其坐标;
关于⊙O的反称点是否存在?若存在,求其坐标;
②点P在直线y=-x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x袖上,求点P的横坐标的取值范围;
(2)⊙C的圆心在x袖上,半径为1,直线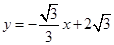 与x轴、y轴分別交于点A,B.若线段AB存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
与x轴、y轴分別交于点A,B.若线段AB存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
先化简,再求值: ,其中x=
,其中x=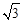 -2.
-2.
解不等式组: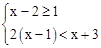
已知抛物线C1的顶点为P(1,0),且过点(0,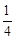 ).将抛物线C1向下平移h个单位(h>0)得到抛物线C2.一条平行于x轴的直线与两条抛物线交于A、B、C、D四点(如图),且点A、C关于y轴对称,直线AB与x轴的距离是m2(m>0).
).将抛物线C1向下平移h个单位(h>0)得到抛物线C2.一条平行于x轴的直线与两条抛物线交于A、B、C、D四点(如图),且点A、C关于y轴对称,直线AB与x轴的距离是m2(m>0).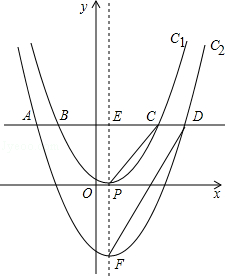
(1)求抛物线C1的解析式的一般形式;
(2)当m=2时,求h的值;
(3)若抛物线C1的对称轴与直线AB交于点E,与抛物线C2交于点F.求证:tan∠EDF﹣tan∠ECP=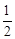 .
.
已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.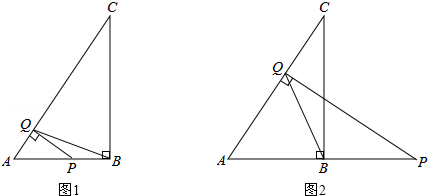
(1)当点P在线段AB上时,求证:△APQ∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.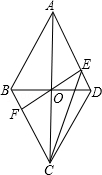
(1)求证:△AOE≌△COF;
(2)若∠EOD=30°,求CE的长.