小明遇到这样一个问题：已知：在△ABC中，AB，BC，AC三边的长分别为
、
、
，求△ABC的面积．
小明是这样解决问题的：如图1所示，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），从而借助网格就能计算出△ABC的面积．他把这种解决问题的方法称为构图法．请回答：
（1）求图1中△ABC的面积；
参考小明解决问题的方法，完成下列问题：
（2）图2是一个6×6的正方形网格（每个小正方形的边长为1）．
①利用构图法在答题卡的图2中画出三边长分别为、
、
的格点△DEF；
②计算△DEF的面积是 ．
（3）如图3，已知△PQR，以PQ，PR为边向外作正方形PQAF，PRDE，连接EF．若PQ=
，PR=，QR=
，求六边形AQRDEF的面积．
（本题5分）观察右图，每个小正方形的边长均为1，
求：图中阴影正方形的面积是多少？它的边长是多少？
（本题10分）化简
（1） 
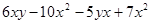
（2）
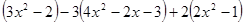
（3）先化简，再求值 ：
，其中
（本题4分）把下列各数在数轴上表示出来，并把它们按从小到大的顺序用“＜”连接起来： 
，－2.5，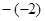
， 
（本题满分14分，其中第（1）题4分，第（2）题的第、小题分别为4分、6分）
如图1，在△ABC中，已知AB=15，cosB=
，tanC=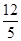
．点D为边BC上的动点（点D不与B、C重合），以D为圆心，BD为半径的⊙D交边AB于点E．
（1）设BD=x，AE=y，求
与
的函数关系式，并写出函数定域义；
（2）如图2，点F为边AC上的动点，且满足BD=
CF，联结DF．
①当△ABC和△FDC相似时，求⊙D的半径；
② 当⊙D与以点F为圆心，FC为半径⊙F外切时，求⊙D的半径．
（本题满分12分，其中第（1）小题5分，第（2）小题4分，第（3）小题3分）
已知抛物线
过点A（-1，0），B（4，0），P（5，3），抛物线与y轴交于点C．
（1）求二次函数的解析式；
（2）求tan∠APC的值；
（3）在抛物线上求一点Q，过Q点作x轴的垂线，垂足为H，使得∠BQH=∠APC．