一球形人造卫星,其最大横截面积为A、质量为m,在轨道半径为R的高空绕地球做圆周运动。由于受到稀薄空气阻力的作用,导致卫星运行的轨道半径逐渐变小。卫星在绕地球运转很多圈之后,其轨道的高度下降了△H,由于△H <<R,所以可以将卫星绕地球运动的每一圈均视为匀速圆周运动。设地球可看成质量为M的均匀球体,万有引力常量为G。取无穷远处为零势能点,当卫星的运行轨道半径为r时,卫星与地球组成的系统具有的势能可表示为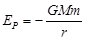 。
。
(1)求人造卫星在轨道半径为R的高空绕地球做圆周运动的周期;
(2)某同学为估算稀薄空气对卫星的阻力大小,做出了如下假设:卫星运行轨道范围内稀薄空气的密度为ρ,且为恒量;稀薄空气可看成是由彼此不发生相互作用的颗粒组成的,所有的颗粒原来都静止,它们与人造卫星在很短时间内发生碰撞后都具有与卫星相同的速度,在与这些颗粒碰撞的前后,卫星的速度可认为保持不变。在满足上述假设的条件下,请推导:
①估算空气颗粒对卫星在半径为R轨道上运行时,所受阻力F大小的表达式;
②估算人造卫星由半径为R的轨道降低到半径为R-△H的轨道的过程中,卫星绕地球运动圈数n的表达式。
如图所示,一高尔夫球运动员从高出水平地面h的坡上水平击出一个高尔夫球,高尔夫球落入距击球点水平距离为L的A穴。不计空气阻力,球半径和A穴的大小远小于h和L。求:
(1)球从被击中到落入A穴所用的时间;
(2)球被击出时初速度的大小;
面积S = 0.2m2、n = 100匝的圆形线圈,处在如图所示的磁场内,磁感应强度随时间t变化的规律是B = 0.02t,R = 3Ω,C = 30μF,线圈电阻r = 1Ω,求:
(1)通过R的电流大小和方向
(2)电容器的电荷量。
如图所示为一列简谐波在t1=0时刻的图象.此时波中质点M的运动方向沿y轴负方向,且t2=0.55 s时质点M恰好第3次到达y轴正方向最大位移处.试求:
(1)此波沿什么方向传播?
(2)波速是多大?
(3)从t1=0至t3=1.2 s,质点N运动的路程和t3时刻相对于平衡位置的位移分别是多少?
如图所示是一种折射率n=1.5的棱镜,现有一束光线沿MN的方向射到棱镜的AB界面上,入射角的正弦值为sin i=0.75.求:
(1)光在棱镜中传播的速率;
(2)通过计算说明此束光线射出棱镜后的方向并画出光路图(不考虑返回到AB面上的光线).
长为L的细线,拴一质量为m的小球,一端固定于O点.让其在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动),如图.求摆线L与竖直方向的夹角为α时:
(1)线的拉力F;
(2)小球运动的线速度的大小;
(3)小球运动的角速度及周期.