知识迁移
我们知道，函数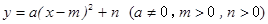
的图像是由二次函数
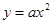的图像向右平移m个单位，再向上平移n个单位得到.类似地，函数
的图像是由反比例函数
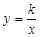的图像向右平移m个单位，再向上平移n个单位得到，其对称中心坐标为（m，n）.
理解应用
函数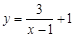
的图像可以由函数
的图像向右平移 个单位，再向上平移 个单位得到，其对称中心坐标为 .
灵活运用
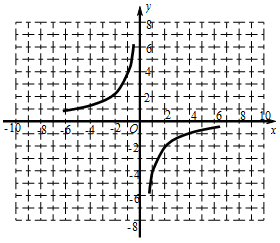
如图，在平面直角坐标系xOy中，请根据所给的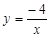
的图像画出函数
的图像，并根据该图像指出，当x在什么范围内变化时，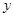
≥
？
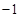实际应用
某老师对一位学生的学习情况进行跟踪研究.假设刚学完新知识时的记忆存留量为1.新知识学习后经过的时间为x，发现该生的记忆存留量随x变化的函数关系为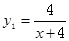
；若在
（
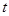≥4）时进行一次复习，发现他复习后的记忆存留量是复习前的2倍（复习时间忽略不计），且复习后的记忆存量随x变化的函数关系为
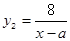.如果记忆存留量为
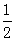时是复习的“最佳时机点”，且他第一次复习是在“最佳时机点”进行的，那么当x为何值时，是他第二次复习的“最佳时机点”？
在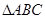
中，AC=25，AB=35，
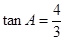，点D为边AC上一点，且AD=5，点E、F分别为边AB上的动点（点F在点E的左边），且∠EDF=∠A.设AE=x，AF=y.
（1）如图1，当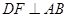
时，求AE的长；
（2）如图2，当点E、F在边AB上时，求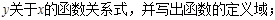
（3）联结CE，当
求
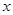的值.
如图，在直角坐标平面内，直线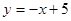
与
轴和
轴分别交于A、B两点，二次函数
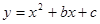的图象经过点A、B，且顶点为C．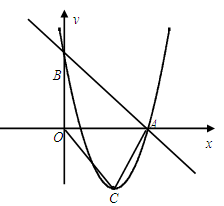
（1）求这个二次函数的解析式；
（2）求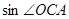
的值；
（3）若P是这个二次函数图象上位于轴下方的一点，且
ABP的面积为10，求点P的坐标．
如图，在正方形ABCD中，E是边CD上一点，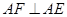
交CB的延长线于点F，联结DF，分别交AE、AB于点G、P.
（1）求证：AE=AF；
（2）若∠BAF=∠BFD,求证：四边形APED是矩形.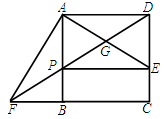
某市对火车站进行了大规模的改建，改建后的火车站除原有的普通售票窗口外，新增了自动打印车票的无人售票窗口．如图,线段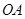
和
分别表示某日从上午8点到上午11点，每个普通售票窗口售出的车票数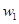
（张）和每个无人售票窗口售出的车票数
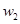（张）关于售票时间
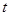（小时）的函数图象．
（1）求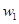（张）与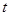（小时）的函数解析式；
（2）若当天开放无人售票窗口个数是普通售票窗口个数的2倍，从上午8点到上午11点，两种窗口共售出的车票数为2400张，求当天开放无人售票窗口的个数？
如图，已知在△ABC中，AB=AC，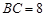
,
，AD⊥BC于D，O是AD上一点，OD=3，以OB为半径的⊙O分别交AB、AC于E、F．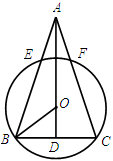
求：（1）⊙O的半径；
（2）BE的长．