已知一次函数
的图像与
轴、
轴分别相交于点A、B，点P在该函数图像上， P到轴、轴的距离分别为
、
。
（1）当P为线段AB的中点时，求
的值；
（2）直接写出的范围，并求当
时点P的坐标；
（3）若在线段AB 上存在无数个P点，使
（
为常数）， 求的值.
如图，在正方形ABCD中，E、F分别是边AB、BC的中点，连接AF、DE相交于点G，连接CG．
（1）求证：AF⊥DE；
（2）求证：CG=CD．
如图，直线y=2x+3与x轴相交于点A，与y轴相交于点B.
（1）求A，B两点的坐标；
（2）过B点作直线BP与x轴相交于P，且使OP=2OA， 求直线BP的解析式.
如图．在△ABC中，D是AB的中点，E是CD的中点，过点C作CF∥AB交AE的延长线于点F，连接BF.
（1）求证：DB=CF；
（2）如果AC=BC．试判断四边行BDCF的形状． 并证明你的结论.
“勤劳”是中华民族的传统美德，我校要求同学们在家里帮助父母做些力所能及的家务. 王刚同学在本学期开学初对部分同学寒假在家做家务的时间进行了抽样调查（时间取整数小时），所得数据统计如下表：
| 时间分组 |
0.5～20.5 |
20.5～40.5 |
40.5～60.5 |
60.5～80.5 |
80.5～100.5 |
| 频数 |
20 |
25 |
30 |
15 |
10 |
（1）抽取样本的容量是.
（2）根据表中数据补全图中的频数分布直方图.
（3）样本的中位数所在时间段的范围是.
（4）若我学校共有学生1600人，那么大约有多少学生在寒假做家务的时间在40.5～100.5小时之间？
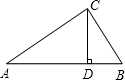
如图，已知在△ABC中，CD⊥AB于D，AC=20，BC=15，DB=9。求AB的长。