下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(3)已知该厂技术改造前 吨甲产品能耗为
吨甲产品能耗为 吨标准煤;试根据(2)求出的线性回归方程,预测生产
吨标准煤;试根据(2)求出的线性回归方程,预测生产 吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(本小题满分12分)
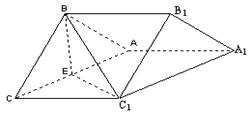
如图,在正三棱柱 .
.
(I)若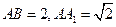 ,求点
,求点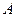 到平面
到平面 的距离;
的距离;

(Ⅱ)当 为何值时,二面角
为何值时,二面角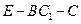 的正弦值为
的正弦值为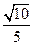 ?
?
(本小题满分12分)
将如下6个函数: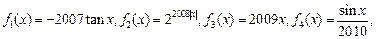
 ,分别写在6张小卡片上,放入盒中.
,分别写在6张小卡片上,放入盒中.
(Ⅰ)现从盒子中任取2张卡片,将卡片上的函数相加得到一个新函数,求所得函数是偶函数的概率;
(Ⅱ)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有奇函数卡片则停止抽取,否则继续进行,求抽取次数 的分布列和数学期望.
的分布列和数学期望.
(本小题满分10分) 锐角三角形ABC的三内角A、B、C所对边的长分别为
锐角三角形ABC的三内角A、B、C所对边的长分别为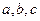 ,设向量
,设向量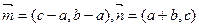 ,且
,且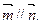
(Ⅰ)求角B的大小;
(Ⅱ)若 ,求
,求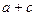 的取值范围.
的取值范围.
(本小题满分12分)
已知A(-3,0),B(3,0),三角形PAB的内切圆的圆心M在直线 上移动。
上移动。
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)某同学经研究作出判断,曲线C在P点处的切线恒过点M,试问:其判断是否正确?若正确,请给出证明;否则说明 理由。
理由。
(示范性高中做)
已知数列 的首项
的首项 前
前 项和为
项和为 ,且
,且
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)令 ,求数列
,求数列 的前n项和
的前n项和 .
.