（本小题满分12分）为了更好的了解某校高三学生期中考试的数学成绩情况，从所有高三学生中抽取40名学生，将他们的数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：[40，50），[50，60），…，[90，100]后得到如图所示的频率分布直方图．
（1）若该校高三年级有1800人，试估计这次考试的数学成绩不低于60分的人数及60分以上的学生的平均分；
（2）若从[40，50）与[90，100]这两个分数段内的学生中随机选取两名学生，求这两名学生成绩之差的绝对值不大于10的概率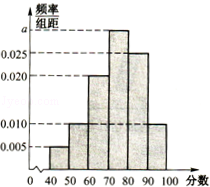
定义：已知函数
在[m，n]（m＜n）上的最小值为t，若t≤m恒成立，则称函数在[m，n] （m＜n）上具有“DK”性质．
（1）判断函数
在[1，2]上是否具有“DK”性质，说明理由；
（2）若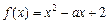
在[a，a＋1]上具有“DK”性质，求a的取值范围．
已知椭圆
（a＞b＞0）的焦距为4，且与椭圆
有相同的离心率，斜率为k的直线l经过点M（0，1），与椭圆C交于不同两点A、B．
（1）求椭圆C的标准方程；
（2）当椭圆C的右焦点F在以AB为直径的圆内时，求k的取值范围．
已知函数
．
（1）求函数
的单调区间；
（2）若在区间[-1，1]上的最大值为6，求在该区间上的最小值
如图，四棱锥P-ABCD的底面为矩形，侧棱PD垂直于底面，PD＝DC＝2BC，E为棱PC上的点，且平面BDE⊥平面PBC．
（1）求证：E为PC的中点；
（2）求二面角A-BD-E的大小．
已知△ABC的周长为6，角A，B，C所对的边a，b，c成等比数列．
（Ⅰ）求角B及边b的最大值；
（Ⅱ）设△ABC的面积为S，求S＋
最大值．