(本小题满分12分)
给定正实数 ,对任意的正整数
,对任意的正整数 ,
, ,其中
,其中 表示不超过实数
表示不超过实数 的最大整数.
的最大整数.
(Ⅰ)若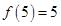 ,求
,求 的取值范围;
的取值范围;
(Ⅱ)求证:(i)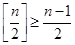 ;
;
(ii)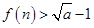 .
.
求下列函数的导数:
(1)

已知f(x)=xlnx,g(x)=-x2+ax-2,
(1)求函数f(x)在[t,t+1](t>0)上的最小值;
(2)存在x0∈[1,e],使得f(x0)≥g(x0)成立,求实数a的取值范围;
已知函数f(x)=x3-3ax-1,a≠0
(1)求f(x)的单调区间;
(2)若f(x)在x=-1处取得极值,直线y=m与y=f(x)的图象有三个不同的交点,求m的取值范围.
某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式 ,其中3<x<6,
,其中3<x<6,
a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求a的值
(2)若该商品的成本为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.
已知函数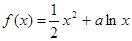 (a∈R).
(a∈R).
(1)若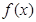 在[1,e]上是增函数,求a的取值范围;
在[1,e]上是增函数,求a的取值范围;
(2)若a=1,1≤x≤e,证明: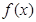 <
<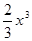 .
.