（本题12分）数学课上，探讨角平分线的作法时，李老师用直尺和圆规作角平分线，方法如下： 
小颖的身边只有刻度尺，经过尝试，她发现利用刻度尺也可以作角平分线．
根据以上情境，解决下列问题：
①李老师用尺规作角平分线时，用到的三角形全等的判定方法是_________．
②小聪的作法正确吗？请说明理由．
③请你帮小颖设计用刻度尺作角平分线的方法．（要求：作出图形，写出作图步骤，不予证明）
经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转，如果这三种情况是等可能的，当三辆汽车经过这个十字路口时：
（1）求三辆车全部同向而行的概率；
（2）求至少有两辆车向左转的概率；
（3）由于十字路口右拐弯处是通往新建经济开发区的，因此交管部门在汽车行驶高峰时段对车流量作了统计，发现汽车在此十字路口向右转的频率为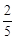
，向左转和直行的频率均为
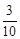．目前在此路口，汽车左转、右转、直行的绿灯亮的时间分别为30秒，在绿灯亮总时间不变的条件下，为了缓解交通拥挤，请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整．
如图1，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．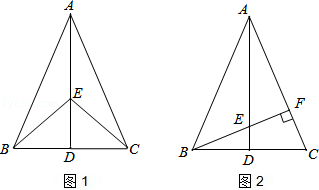
（1）求证：BE=CE；
（2）如图2，若BE的延长线交AC于点F，且BF⊥AC，垂足为F，∠BAC=45°，原题设其它条件不变．求证：△AEF≌△BCF．
（1）计算：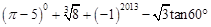
（2）化简求值：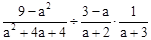
，其中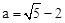
．
如图所示，直线l：y=3x+3与x轴交于点A，与y轴交于点B．把△AOB沿y轴翻折，点A落到点C，抛物线过点B、C和D（3，0）．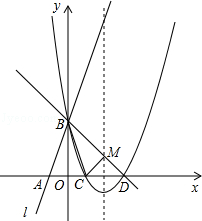
（1）求直线BD和抛物线的解析式．
（2）若BD与抛物线的对称轴交于点M，点N在坐标轴上，以点N、B、D为顶点的三角形与△MCD相似，求所有满足条件的点N的坐标．
（3）在抛物线上是否存在点P，使S△PBD=6？若存在，求出点P的坐标；若不存在，说明理由．
如图所示，AB是⊙O的直径，AE是弦，C是劣弧AE的中点，过C作CD⊥AB于点D，CD交AE于点F，过C作CG∥AE交BA的延长线于点G．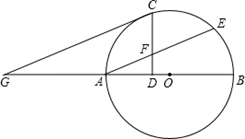
（1）求证：CG是⊙O的切线．
（2）求证：AF=CF．
（3）若∠EAB=30°，CF=2，求GA的长．