若︱x-1︱+︱y+2︱=0,求x+y的值
(本小题8分)已知反比例函数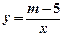 的图象经过点A(1,3).
的图象经过点A(1,3).
求:(Ⅰ)m的值和这个函数的解析式;
(Ⅱ)当-3<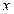 <-1时,对应的函数
<-1时,对应的函数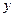 的取值范围.
的取值范围.
(本小题6分)解不等式组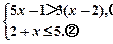
(本题满分10分)
已知:如图,在△ABC中,D为BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于点G,DE⊥GF,并交AB于点E,连结EG.
(1)求证BG=CF;
(2)试猜想BE+CF与EF的大小关系,并加以证明.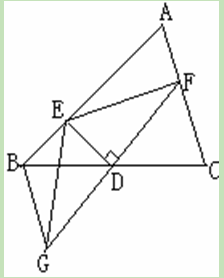
(本题满分8分)
我市某化工厂现有甲种原料290千克,乙种原料212千克,计划利用这两种原料生产A、B两种产品共80件,生产一件A产品需要甲种原料5千克 ,乙种原料1.5千克;生产一件B种产品需要甲种原料2.5千克,乙种原料3.5千克,该化工厂现有的原料能否保证生产顺利进行?若能的话,有几种方案?请你设计出来。
,乙种原料1.5千克;生产一件B种产品需要甲种原料2.5千克,乙种原料3.5千克,该化工厂现有的原料能否保证生产顺利进行?若能的话,有几种方案?请你设计出来。
(本题满分8分)
某中学为八年级寄宿学生安排宿舍,如果每间4人,那么有20人无法安排,如果每间8人,那么有一间不空也不满,求宿舍间数和寄宿学生人数。