(本小题满分16分)已知二次函数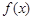 满足
满足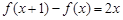 且
且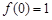 .
.
(1)求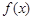 的解析式;
的解析式;
(2)当 时,不等式:
时,不等式: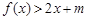 恒成立,求实数
恒成立,求实数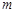 的范围.
的范围.
(3)设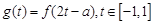
 ,求
,求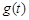 的最大值;
的最大值;
(本小题满分12分)如图,在四棱锥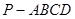 中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点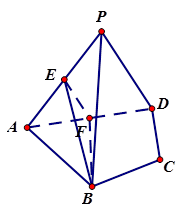
求证:(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD
(本小题满分12分)已知两直线l1:x+my+6=0 l2:(m-2)x+3my+2m=0
当m为何值时,l1与l2:
(1)平行;(2)垂直;
(本小题满分10分) 已知P(3,2),一直线 过点P,
过点P,
①若直线 在两坐标轴上截距之和为12,求直线
在两坐标轴上截距之和为12,求直线 的方程;
的方程;
②若直线 与x、y轴正半轴交于A、B两点,当
与x、y轴正半轴交于A、B两点,当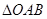 面积为12时求直线
面积为12时求直线 的方程.
的方程.
已知函数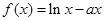 在
在 处的切线
处的切线 与直线
与直线 平行.
平行.
(1)求实数 的值;
的值;
(2)若关于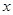 的方程
的方程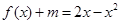 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数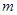 的取值范围;
的取值范围;
(3)记函数 ,设
,设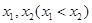 是函数
是函数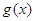 的两个极值点,若
的两个极值点,若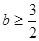 ,且
,且 恒成立,求实数
恒成立,求实数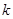 的最大值.
的最大值.
已知椭圆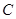 :
: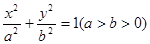 的离心率为
的离心率为 ,右焦点为(
,右焦点为(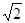 ,0).
,0).
(1)求椭圆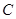 的方程;
的方程;
(2)若过原点 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆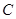 交于
交于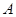 ,
, 两点,求证:点
两点,求证:点 到直线
到直线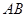 的距离为定值.
的距离为定值.