(本小题满分10分)
设 是一个公差为
是一个公差为 的等差数列,它的前10项和
的等差数列,它的前10项和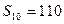 且
且 ,
, ,
, 成等比数列,求公差
成等比数列,求公差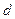 的值和数列
的值和数列 的通项公式.
的通项公式.
本小题满分8分)
已知锐角△ABC的三内角 所对的边分别为
所对的边分别为 ,边a、b是方程
,边a、b是方程
x2-2 x+2=0的两根,角A、B满足关系2sin(A+B)-
x+2=0的两根,角A、B满足关系2sin(A+B)- =0,求角C的度数,边c的长度及△ABC的面积.
=0,求角C的度数,边c的长度及△ABC的面积.
(本小题满分8分)
已知关于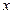 的不等式
的不等式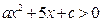 的解集为
的解集为 ,求关于
,求关于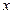 的不等式
的不等式 的解集.
的解集.
已知定义在区间(0,+∞)上的函数f(x)满足 -
- .当x>1时,f(x)<0.
.当x>1时,f(x)<0.
(1)求f(1)的值;
(2)判断f(x)单调性;
(3)若f(3)=-1,解不等式f(x)<2.
已知函数f(x)满足f(x+y)=f(x)·f(y),且f(1)=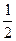 .
.
(1)当n∈N*时,求f(n)的表达式;
(2)当an=n·f(n), n∈N*,求证a1+a2+…+an<2;
(3)设bn=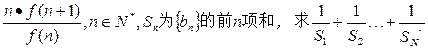 .
.