已知椭圆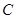 的中心在原点
的中心在原点 ,离心率为
,离心率为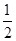 ,它的一个短轴端点恰好是抛物线
,它的一个短轴端点恰好是抛物线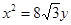 的焦点.
的焦点.
(1)求椭圆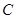 的标准方程;
的标准方程;
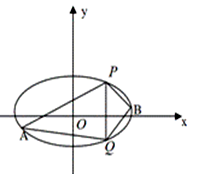
(2)已知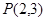 ,
,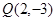 是椭圆上的两点,
是椭圆上的两点,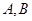 是椭圆上位于直线
是椭圆上位于直线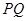 两侧的动点,当
两侧的动点,当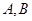 运动时,满足
运动时,满足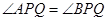 ,试问:直线
,试问:直线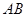 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
数列 中,已知
中,已知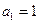 ,且
,且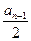 是1与
是1与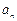
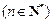 的等差中项.
的等差中项.
(Ⅰ)求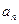 ;
;
(Ⅱ)设 ,记数列
,记数列 的前
的前 项和为
项和为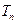 ,证明:
,证明: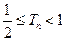
在△ ABC中, BC= , , .
(Ⅰ)求 AB的值; 

(Ⅱ)求
的值.
已知α=1690o,
(1)把α表示成2kπ+β的形式(k∈Z,β∈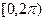 ).
).
(2)求θ,使θ与α的终边相同,且θ∈(- 4π,- 2π).
直角坐标系xoy中,角 的始边为x轴的非负半轴,终边为射线l:y=
的始边为x轴的非负半轴,终边为射线l:y= x (x≥0).
x (x≥0).
(1)求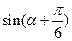 的值;
的值;
(2)若点P,Q分别是角 始边、终边上的动点,且PQ=4,求△POQ面积最大时,点P,Q的坐标.
始边、终边上的动点,且PQ=4,求△POQ面积最大时,点P,Q的坐标.
已知数列 的前n项和
的前n项和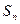 满足
满足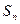 =
=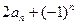 ,
,
(1)写出数列 的前3项
的前3项 ;
;
(2)求数列 的通项公式
的通项公式
(3)证明:对于任意的整数 ,有
,有