甲、乙两车在平直公路上比赛,某一时刻,乙车在甲车前方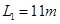 处,乙车速度
处,乙车速度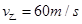 ,甲车速度
,甲车速度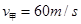 ,此时乙车离终点尚有
,此时乙车离终点尚有 的距离,如图所示,若甲车做匀加速直线运动,加速度
的距离,如图所示,若甲车做匀加速直线运动,加速度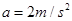 ,乙车速度不变,不计车长,求:
,乙车速度不变,不计车长,求: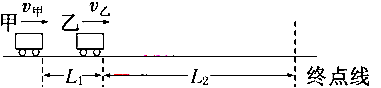
(1)经过多长时间甲、乙两车间距离最大,最大距离是多少
(2)试通过计算说明到达终点前甲车能否超过乙车
图示为修建高层建筑常用的塔式起重机。在起重机将质量m=5×103 kg的重物竖直吊起的过程中,重物由静止开始向上作匀加速直线运动,加速度a="0.2" m/s2,当起重机输出功率达到其允许的最大值时,保持该功率直到重物做vm="1.02" m/s的匀速运动。取g="10" m/s2,不计额外功。求:
(1)起重机允许输出的最大功率。
(2)重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率。
(16分)图示为修建高层建筑常用的塔式起重机.在起重机将质量m=5×103kg的重物竖直吊起的过程中,重物由静止开始向上做匀加速直线运动,加速度a="0.2" m/s2,当起重机输出功率达到其允许的最大值时,保持该功率直到重物做vm="1.02" m/s的匀速运动.取g="10" m/s2,不计额外功.求:
(1)起重机允许输出的最大功率.
(2)重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率.
(12分)如图所示,建筑工人通过滑轮装置将一质量是100 kg的料车沿30°角的斜面由底端匀速地拉到顶端,斜面长L是4 m,若不计滑轮的质量和各处的摩擦力,g取10 N/kg,求这一过程中: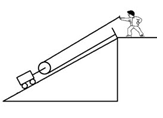
(1)人拉绳子的力做的功;
(2)物体的重力做的功;
(3)物体受到的各力对物体做的总功.
(2011年南京质检)如图所示为“S”形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成的,固定在竖直平面内,轨道弯曲部分是由两个半径相等的半圆连接而成的,圆半径比细管内径大得多,轨道底端与水平地面相切,弹射装置将一个小球(可视为质点)从a点水平射向b点并进入轨道,经过轨道后从p点水平抛出,已知小球与地面ab段间的动摩擦因数μ=0.2,不计其他机械能损失,ab段长L=1.25 m,圆的半径R=0.1 m,小球质量m=0.01 kg,轨道质量为M=0.15 kg,g=10 m/s2,求:
(1)若v0=5 m/s,小球从p点抛出后的水平射程;
(2)若v0=5 m/s,小球经过轨道的最高点时,管道对小球作用力的大小和方向;
(3)设小球进入轨道之前,轨道对地面的压力大小等于轨道自身的重力,当v0至少为多大时,轨道对地面的压力为零.
如图甲所示,在倾角为30°的足够长光滑斜面AB前,有一粗糙水平面OA,OA长为4 m.有一质量为m的滑块,从O处由静止开始受一水平向右的力F作用.F按图乙所示的规律变化.滑块与OA间的动摩擦因数μ=0.25,g取10 m/s2,试求:
(1)滑块到A处的速度大小;
(2)不计滑块在A处的速率变化,滑块冲上斜面AB的长度是多少?