(16分)图示为修建高层建筑常用的塔式起重机.在起重机将质量m=5×103 kg的重物竖直吊起的过程中,重物由静止开始向上做匀加速直线运动,加速度a="0.2" m/s2,当起重机输出功率达到其允许的最大值时,保持该功率直到重物做vm="1.02" m/s的匀速运动.取g="10" m/s2,不计额外功.求:
(1)起重机允许输出的最大功率.
(2)重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率.
从离地面125m高的空中从静止释放一小球,小球自由落下,取g=10m/s2,求:(1)小球经过多长时间落到地面;
(2)自开始下落计时,小球最后1s内的位移。
一列士兵的队伍长120m,正以某一速度做匀速直线运动,因有紧急情况需要通知排头士兵,一名通讯员以不变的速率跑步从队尾赶到队头,又从队头返回队尾,在此过程中队伍前进了288m,求通讯员在这段往返时间内共走了多少m?
一矿井深为125m,在矿井口每隔一定时间自由落下一小球,当第11个小球刚从矿井口下落时,第一个小球恰好到达井底,则:
(1)相邻小球开始下落的时间间隔为多少?
(2)这时第3个小球和第5个小球相距多远?
2014年2月,第22届冬奥会在俄罗斯索契成功举行。在高山滑雪速降比赛中,运动员由静止开始沿滑道向下做匀加速直线运动,2s内的位移为8m。在此过程中
(1)求运动员的加速度大小;
(2)求2s末运动员的速度大小;
如图所示,某工厂传送带装置倾斜放置,倾角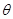 =37o,传送带AB长度xo=l0m。有一水平平台CD高度保持6.45m不变。现调整D端位置,当D、B的水平距离合适时,自D端水平抛出的物体恰好从B点沿BA方向冲上斜面,此后D端固定不动,g=l0m/s2。另外,传送带B端上方安装一极短的小平面,与传送带AB平行共面,保证自下而上传送的物体能沿AB方向由B点斜向上抛出。(sin37o=0.6,cos37o=0.8)
=37o,传送带AB长度xo=l0m。有一水平平台CD高度保持6.45m不变。现调整D端位置,当D、B的水平距离合适时,自D端水平抛出的物体恰好从B点沿BA方向冲上斜面,此后D端固定不动,g=l0m/s2。另外,传送带B端上方安装一极短的小平面,与传送带AB平行共面,保证自下而上传送的物体能沿AB方向由B点斜向上抛出。(sin37o=0.6,cos37o=0.8)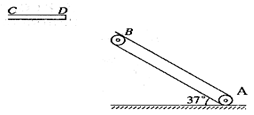
(1)求D、B的水平距离;
(2)若传送带以5m/s的速度逆时针匀速运行,某物体甲与传送带间动摩擦因数μ1=0.9,自A点沿传送带方向以某一初速度冲上传送带时,恰能水平落到水平台的D端,求物体甲的最大初速度vo1。
(3)若传送带逆时针匀速运行,某物体乙与传送带间动摩擦因数μ2=0.6,自A点以vo2=11m/s的初速度沿传送带方向冲上传送带时,恰能水平落到水平台的D端,求传送带的速度v′。