已知实数x、y、z满足x+2y+3z=1，则x2+y2+z2的最小值为．
设向量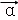
=（a，b），
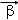=（m，n），其中a，b，m，n∈R，由不等式|
|
•|
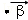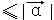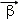|恒成立，可以证明（柯西）不等式（am+bn）2≤（a2+b2）（m2+n2）（当且仅当
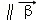，即an=bm时等号成立），己知x，y∈R+，若
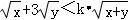恒成立，利用柯西不等式可求得实数k的取值范围是．
已知a、b、c、d均为正数，且a2+b2=4，cd=1，则（a2c2+b2d2）（b2c2+a2d2）的最小值为．
若a，b，c为正实数且满足a+2b+3c=6，则
+
+
的最大值为．
已知a，b，c∈R，且2a+2b+c=8，则（a﹣1）2+（b+2）2+（c﹣3）2的最小值是．
的不等式
的解集不是空集，则实数
的取值范围是 ．