(本小题满分12分)
甲厂以x千克/小时的速度匀速生产某种产品(生产条件要求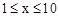 ),每小时可获得利润是
),每小时可获得利润是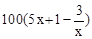 元.
元.
(1)要使生产该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求最大利润.
(本小题满分12分)如图所示,正方形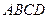 与直角梯形
与直角梯形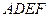 所在平面互相垂直,
所在平面互相垂直,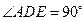 ,
,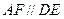 ,
,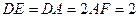 .
.
(Ⅰ)求证: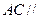 平面
平面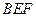 ;
;
(Ⅱ)求四面体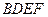 的体积.
的体积.
(本小题满分12分)在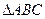 中,角
中,角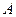 、
、 、
、 所对的边分别为
所对的边分别为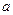 、
、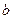 、
、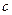 ,若向量
,若向量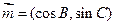 ,
, ,且
,且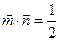
(Ⅰ)求角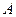 的大小
的大小
(Ⅱ)若 ,
,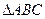 的面积
的面积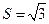 ,求
,求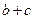 的值
的值
已知函数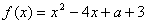 ,
,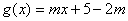 .
.
(1)若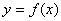 在
在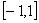 上存在零点,求实数
上存在零点,求实数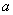 的取值范围;
的取值范围;
(2)当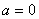 时,若对任意的
时,若对任意的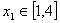 ,总存在
,总存在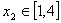 ,使
,使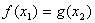 ,求实数
,求实数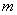 的取值范围.
的取值范围.
医学上为了研究传染病在传播的过程中病毒细胞的生长规律及其预防措施,将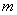 个病毒细胞注入到一只小白鼠的体内进行试验.在试验过程中,得到病毒细胞的数量与时间的关系记录如下表:
个病毒细胞注入到一只小白鼠的体内进行试验.在试验过程中,得到病毒细胞的数量与时间的关系记录如下表:
| 时间(小时) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 病毒细胞总数(个) |
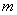 |
2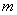 |
4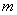 |
8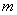 |
16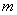 |
32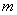 |
64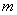 |
已知该种病毒细胞在小白鼠体内超过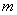
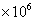 个时,小白鼠将死亡,但有一种药物对杀死此种病毒有一定效果,用药后,即可杀死其体内的大部分病毒细胞.
个时,小白鼠将死亡,但有一种药物对杀死此种病毒有一定效果,用药后,即可杀死其体内的大部分病毒细胞.
(1)在16小时内,写出病毒细胞的总数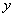 与时间
与时间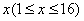 的函数关系式;
的函数关系式;
(2)为了使小白鼠在实验过程中不死亡,最迟应在何时注射该种药物.(精确到整数,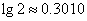 )
)
已知函数f(x)对一切x,y∈R,都有f(x+y)=f(x)+f(y).
(1)求f(0)的值
(2)求证:f(x)是奇函数;
(3)若f(-3)=a,用a表示f(12).