已知函数 .
.
(1)若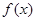 在
在 上是增函数,求
上是增函数,求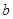 的取值范围;
的取值范围;
(2)若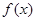 在
在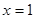 处取得极值,且
处取得极值,且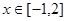 时,
时,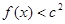 恒成立,求
恒成立,求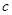 的取值范围.
的取值范围.
观察下列三角形数表:
第一行
第二行
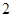
第三行
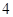

第四行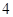
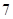
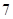
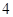
第五行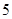
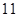

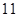
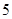
………………………………………….
假设第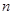 行的第二个数为
行的第二个数为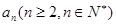 .
.
(1)依次写出第八行的所有8个数字;
(2)归纳出 的关系式,并求出
的关系式,并求出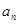 的通项公式.
的通项公式.
用分析法证明: .
.
有一道数学难题,在半小时内,甲能解决它的概率为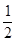 ,乙能解决它的概率为
,乙能解决它的概率为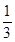 ,两人试图独立地在半小时内解决它,求:
,两人试图独立地在半小时内解决它,求:
(1)两人都未解决的概率;
(2)问题得到解决的概率.
已知定义在区间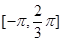 上的函数
上的函数 的图像关于直线
的图像关于直线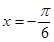 对称,当
对称,当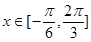 时,函数
时,函数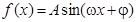
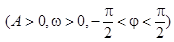 的图像如下图所示。
的图像如下图所示。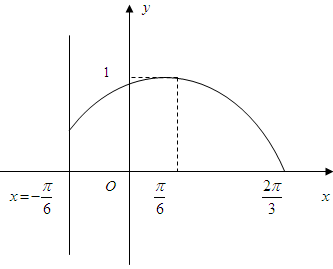
(Ⅰ) 求函数 在
在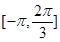 上的解析式;
上的解析式;
|
(Ⅱ) 求方程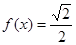 的解.
的解.