设椭圆E的方程为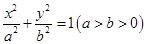 ,点O为坐标原点,点A的坐标为
,点O为坐标原点,点A的坐标为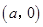 ,点B的坐标为
,点B的坐标为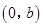 ,点M在线段AB上,满足
,点M在线段AB上,满足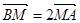 ,直线OM的斜率为
,直线OM的斜率为 .
.
(I)求E的离心率e;
(II)设点C的坐标为 ,N为线段AC的中点,点N关于直线AB的对称点的纵坐标为
,N为线段AC的中点,点N关于直线AB的对称点的纵坐标为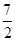 ,求E的方程.
,求E的方程.
已知函数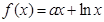 ,函数
,函数 的导函数
的导函数 ,且
,且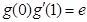 ,其中
,其中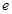 为自然对数的底数.
为自然对数的底数.
(1)求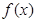 的极值;
的极值;
(2)若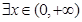 ,使得不等式
,使得不等式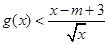 成立,试求实数
成立,试求实数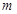 的取值范围;
的取值范围;
如图,在四棱锥E﹣ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点
(1)求证:DE∥平面FGH;
(2)若点P在直线GF上,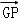 =λ
=λ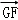 ,且二面角D﹣BP﹣A的大小为
,且二面角D﹣BP﹣A的大小为 ,求λ的值.
,求λ的值.
数列 的前
的前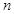 项和记为
项和记为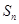 ,
, ,
,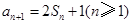 .
.
(1)求证 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;
(2)等差数列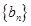 的各项为正,其前
的各项为正,其前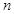 项和为
项和为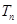 ,且
,且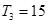 ,又
,又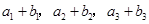 成等比数列,求
成等比数列,求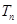 .
.
已知△ABC的内角A,B,C所对的边分别为a,b,c,且a=2,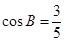 .
.
(1)若b=4,求sin A的值;
(2)若△ABC的面积S△ABC=4,求b,c的值.
已知圆C:x2+y2+2x-4y+3=0,若圆C的切线在x轴、y轴上的截距相等,求切线的方程.